Advertisements
Advertisements
Question
It is a common observation that rain clouds can be at about a kilometre altitude above the ground.
- If a rain drop falls from such a height freely under gravity, what will be its speed? Also calculate in km/h. ( g = 10 m/s2)
- A typical rain drop is about 4mm diameter. Momentum is mass x speed in magnitude. Estimate its momentum when it hits ground.
- Estimate the time required to flatten the drop.
- Rate of change of momentum is force. Estimate how much force such a drop would exert on you.
- Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5 cm.
(Assume that umbrella is circular and has a diameter of 1 m and cloth is not pierced through !!)
Advertisements
Solution
Given, height (h) = 1 km = 100 m
g = 10 m/s2
a. Velocity attained by the raindrop in freely falling through a height h.
v = `sqrt(2gh)`
= `sqrt(2 xx 10 xx 1000)`
= `100sqrt(2)` m/s
= `100sqrt(2) xx (60 xx 60)/1000` km/h
= `360sqrt(2)` km/h ≈ 510 km/h
b. Diameter of the drop (d) = 2r = 4 mm
∴ Radius of the drop (r) = 2 mm = 2 × 10–3 m
Mass of a raindrop (m) = V × p
= `4/3 pir^3p`
= `4/3 xx 22/7 xx (2 xx 10^-3)^3 xx 10^3` .....(∵ Density of water = 103 kg/m3)
= 3.4 × 10–5 kg
The momentum of the raindrop (p) = mv
= `3.4 xx 10^-5 xx 100sqrt(2)`
= `4.7 xx 10^-3` kg-m/s
≈ `5 xx 10^-3` kg-m/s
c. Time required to fatten the drop = time taken by the drop to travel the distance equal to the diameter of the drop near the ground
`t = d/v`
= `(4 xx 10^3)/(100 sqrt(2))`
= ``0.028 xx 10^-3` s
= `2.8 xx 10^-5` s ≈ 30 ms
d. Force exerted by a raindrop
F = `"Change in momentum"/"Time"`
= `(p - 0)/t`
= `(4.7 xx 10^-3)/(2.8 xx 10^-5)` ≈ 168 N
e. Radius of the umbrella (R) = `1/2` m
∴ Area of the umbrella (A) = `piR^2`
= `22/7 xx (1/2)^2`
= `22/28`
= `11/4 ≈ 0.8` m2
Number of drops striking the umbrella simultaneously with an average separation of 5 cm = `5 xx 10^-2` m
= `0.8/(5 xx 10^-2)^2` = 320
∴ Net force exerted on umbrella = 320 × 168 = 53760 N ≈ 54000 N.
APPEARS IN
RELATED QUESTIONS
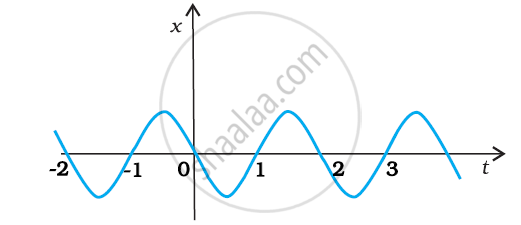
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
A person travelling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s2 to his scooter. How far will it travel before stopping?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the maximum speed attained by the train .
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
A popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situated at a distance of 2.0 m from the goli of the second player. This second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middle fingers and making the throw. If the projected goli hits the goli of the first player, the second player wins. If the height from which the goli is projected is 19.6 cm from the ground and the goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationery goli without falling on the ground earlier?
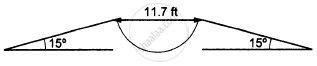
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the truck .
The benches of a gallery in a cricket stadium are 1 m wide and 1 m high. A batsman strikes the ball at a level one metre above the ground and hits a mammoth sixer. The ball starts at 35 m/s at an angle of 53° with the horizontal. The benches are perpendicular to the plane of motion and the first bench is 110 m from the batsman. On which bench will the ball hit?
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beat a drum and B hears the sound t1 time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum timer after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in travelling between the friends.
