Advertisements
Advertisements
Question
A car moving along a straight highway with a speed of 126 km h–1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?
Solution
Initial velocity of the car, u = 126 km/h =`(126xx1000)/(60xx60)` ms-1 35 m/s
Final velocity of the car, v = 0
Distance covered by the car before coming to rest, s = 200 m
Retardation produced in the car = a
From third equation of motion, a can be calculated as:
`v^2 - u^2 = 2as`
∴ `(0)^2 - (35)^2 = 2 xx a xx 200`
`a = (35 xx 35)/(2xx200) = -3.06 "m/s"^2`
From first equation of motion, time (t) taken by the car to stop can be obtained as:
v = u + at
`t = (v-u)/a = (-35)/-3.06 = 11.44 s`
APPEARS IN
RELATED QUESTIONS
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
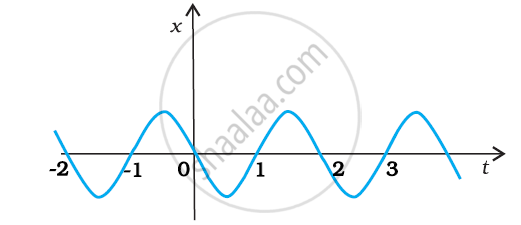
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
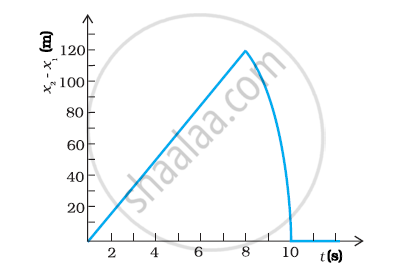
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in Fig. 3.27 correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s2. Give the equations for the linear and curved parts of the plot.
At which point on its path a projectile has the smallest speed?
A driver takes 0.20 s to apply the brakes after he sees a need for it. This is called the reaction time of the driver. If he is driving a car at a speed of 54 km/h and the brakes cause a deceleration of 6.0 m/s2, find the distance travelled by the car after he sees the need to put the brakes on.
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
A stone is thrown vertically upward with a speed of 28 m/s.Find its velocity one second before it reaches the maximum height.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
