Advertisements
Advertisements
प्रश्न
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of 1 m/s2 and the projection velocity in the vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
उत्तर
Given:
Acceleration of the car = 1 m/s2
Projection velocity of the ball (considered as a projectile) in the vertical direction = 9.8 m/s
Angle of projection, α = 90˚
Let u be the initial velocity of the car when the ball is thrown.
Both the car and the ball have the same horizontal velocity.
We know that the distance travelled by the ball in horizontal direction is given by -s = ut
Here, t is the time.
Also, the distance travelled by the car in horizontal direction is given by
Therefore, the ball drops 2 m behind the boy.
APPEARS IN
संबंधित प्रश्न
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
A ball is projected vertically upward with a speed of 50 m/s. Find the speed at half the maximum height. Take g = 10 m/s2.
A stone is thrown vertically upward with a speed of 28 m/s.Find its velocity one second before it reaches the maximum height.
A person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the positions of the 3rd, 4th and 5th ball when the 6th ball is being dropped.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
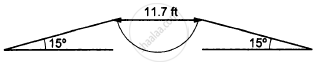
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
A ball is projected from a point on the floor with a speed of 15 m/s at an angle of 60° with the horizontal. Will it hit a vertical wall 5 m away from the point of projection and perpendicular to the plane of projection without hitting the floor? Will the answer differ if the wall is 22 m away?
Find the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with a speed u at an angle θ with the horizontal.
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the truck .
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. Find the time taken by the boat to reach the opposite bank.
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
It is a common observation that rain clouds can be at about a kilometre altitude above the ground.
- If a rain drop falls from such a height freely under gravity, what will be its speed? Also calculate in km/h. ( g = 10 m/s2)
- A typical rain drop is about 4mm diameter. Momentum is mass x speed in magnitude. Estimate its momentum when it hits ground.
- Estimate the time required to flatten the drop.
- Rate of change of momentum is force. Estimate how much force such a drop would exert on you.
- Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5 cm.
(Assume that umbrella is circular and has a diameter of 1 m and cloth is not pierced through !!)
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15 m at t = 2 s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
