Advertisements
Advertisements
प्रश्न
A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.
Advertisements
उत्तर १
Ball is dropped from a height, s = 90 m
Initial velocity of the ball, u = 0
Acceleration, a = g = 9.8 m/s2
Final velocity of the ball = v
From second equation of motion, time (t) taken by the ball to hit the ground can be obtained as:
`s = ut + 1/2 at^2`
`90 = 0 + 1/2 xx 9.8t^2`
`t = sqrt(18.38) = 4.29 s`
From first equation of motion, final velocity is given as:
v = u + at
= 0 + 9.8 × 4.29 = 42.04 m/s
Rebound velocity of the ball, ur = `9/10v = 9/10 xx 42.04 = 37.84 "m/s"`
Time (t) taken by the ball to reach maximum height is obtained with the help of first equation of motion as:
v = ur + at′
0 = 37.84 + (– 9.8) t′
t' = (-37.84)/-9.8 = 3.86 s
Total time taken by the ball = t + t′ = 4.29 + 3.86 = 8.15 s
As the time of ascent is equal to the time of descent, the ball takes 3.86 s to strike back on the floor for the second time.
The velocity with which the ball rebounds from the floor = `9/10xx37.84 = 34.06 "m/s"`
Total time taken by the ball for second rebound = 8.15 + 3.86 = 12.01 s
The speed-time graph of the ball is represented in the given figure as:
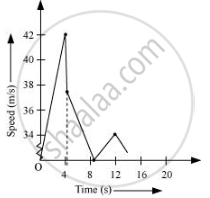
उत्तर २
u = 0, a = 10 ms-2, S = 90 m, t = ?, v = ?
Using `v^2 - u^2 = 2as, v^2 - (0)^2 = 2xx10xx90`
=> v = `30sqrt2` "m/s"
Again using `S = ut + 1/2at^2, 90 = 0 xx t + 1/2 xx 10t^2`
`=> t= sqrt18 s = 3sqrt2 s`
Rebound velocity = `9/10 xx 30sqrt2 ms^(-1) = 27sqrt2 ms^(-1)`
Time taken to reach highest point = `(27sqrt2)/10` s = `2.7sqrt2` s
Total time = `(3sqrt2 + 2.7sqrt2)s = 5.7sqrt2 s`
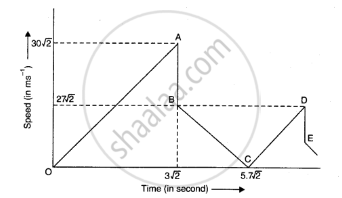
OA represents the vertically downward motion after the ball has been dropped from a height of 90m. The reaches the floor with a velocity of `30sqrt2 ms^(-1)` after having been in motion for `3sqrt2 s`. The verticle straight portion AB represent the loss of 1/10 th of speed, BC represents the vertically upward motion after first rebound. The ball reaches the highest point in `27sqrt2`s. The total time from the beginning is `3sqrt2+2.7sqrt2` i.e `5.7sqrt2` s.
C represent the highest point reached after first rebound. CD represent the vertically downward motion. D represents the situation when the ball again reaches the floor DE represent the loss of speed.
APPEARS IN
संबंधित प्रश्न
A car moving along a straight highway with a speed of 126 km h–1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
At which point on its path a projectile has the smallest speed?
In a projectile motion the velocity
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A stone is thrown vertically upward with a speed of 28 m/s. change if the initial speed is more than 28 m/s such as 40 m/s or 80 m/s ?
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
A popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situated at a distance of 2.0 m from the goli of the second player. This second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middle fingers and making the throw. If the projected goli hits the goli of the first player, the second player wins. If the height from which the goli is projected is 19.6 cm from the ground and the goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationery goli without falling on the ground earlier?
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
Find the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with a speed u at an angle θ with the horizontal.
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the road.
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the time taken by the plane to go from A to B.
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beat a drum and B hears the sound t1 time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum timer after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in travelling between the friends.
