Advertisements
Advertisements
प्रश्न
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15 m at t = 2 s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
उत्तर
Let the speeds of the two balls (1 and 2) be v1 and v2 where
If v1 = 2v, v2 = v
If y1 and y2 and the distance covered by balls 1 and 2, respectively before coming to rest then
`y_1 = v_1^2/(2g) = (4v^2)/(2g)` and `y_2 = (v_2^2)/(2g) = v^2/(2g)`
Since, `y_1 - y_2 = 15 m (4v^2)/(2g) - v^2/(2g)` = 15 m or `(3v^2)/(2g)` = 15 m
or `v^2 = sqrt(5m xx (2 xx 10))` m/s2
or v = 10 m/s
Clearly, v1 = 20 m/s and v2 = 10 m/s
As `y_1 = v_1^2/(2g) = (20 m)^2/(2 xx 10 m 15)` = 20 m
`y_2 - y_1 - 15` m = 5 m
It t2 is the time taken by the ball 2 toner a distance of 5 m, then from `y_2 = v_2^t - 1/2 "gt"_2^2`
5 = `10t_2 - 5t_2^2` or `t_2^2 - 2t_2 + 1` = 0
Where t2 = 15
Since t1 (time taken by ball 1 to cover the distance of 20 m) is 2s, the time interval between the two throws
= t1 – t2
= 2s – 1s
= 1s
APPEARS IN
संबंधित प्रश्न
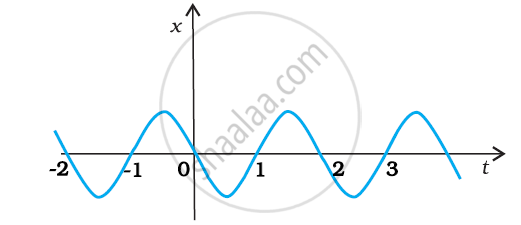
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A ball is projected vertically upward with a speed of 50 m/s. Find the time to reach the maximum height .
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the maximum height reached .
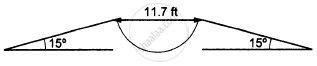
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
Find the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with a speed u at an angle θ with the horizontal.
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
