Advertisements
Advertisements
प्रश्न
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
उत्तर
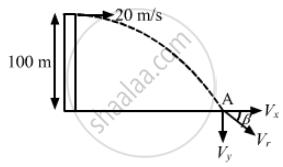
Given:
Speed of the ball, ux = 20 m/s
Height from which the ball is dropped, h = 100 m
We know that horizontal velocity remains constant throughout the motion of the ball.
At A, vx = 20 m/s.
vy = u + gt = 0 + 9.8 × 4.5
⇒vy = 44.1 m/s
Resultant velocity:
\[v_r = \sqrt{\left( 44 . 1 \right)^2 + \left( 20 \right)^2} \approx 49 \text{ m } /s\]
\[\tan \beta = \frac{v_y}{v_x} = \frac{44 . 1}{20} = 2 . 205\]
\[ \Rightarrow \beta = \tan^{- 1} \left( 2 . 205 \right) = 66^\circ \]
Therefore, the ball strikes the ground with a magnitude of velocity 49 m/s and the direction at an angle of 66° with the ground.
APPEARS IN
संबंधित प्रश्न
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the average velocity during this period .
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the distance travelled by the particle during this period.
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball is sand assuming it to be uniform.
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the maximum height reached .
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
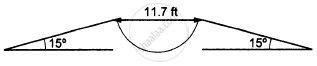
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
Find the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with a speed u at an angle θ with the horizontal.
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of 1 m/s2 and the projection velocity in the vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
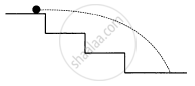
A staircase contains three steps each 10 cm high and 20 cm wide (in the following figure). What should be the minimum horizontal velocity of a ball rolling of the uppermost plane so as to hit directly the lowest plane ?
The benches of a gallery in a cricket stadium are 1 m wide and 1 m high. A batsman strikes the ball at a level one metre above the ground and hits a mammoth sixer. The ball starts at 35 m/s at an angle of 53° with the horizontal. The benches are perpendicular to the plane of motion and the first bench is 110 m from the batsman. On which bench will the ball hit?
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. Find the time taken by the boat to reach the opposite bank.
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation x. What will be the time B finds between seeing and hearing the drum beating by A?
A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
