Advertisements
Advertisements
Question
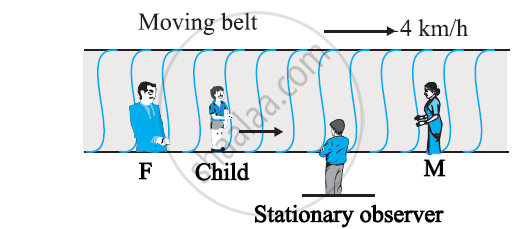
On a long horizontally moving belt (Fig. 3.26), a child runs to and fro with a speed 9 km h–1 (with respect to the belt) between his father and mother located 50 m apart on the moving belt. The belt moves with a speed of 4 km h–1. For an observer on a stationary platform outside, what is the
(a) speed of the child running in the direction of motion of the belt ?.
(b) speed of the child running opposite to the direction of motion of the belt ?
(c) time taken by the child in (a) and (b) ?
Which of the answers alter if motion is viewed by one of the parents?
Solution 1
(a) Speed of the belt, vB = 4 km/h
Speed of the boy, vb = 9 km/h
Since the boy is running in the same direction of the motion of the belt, his speed (as observed by the stationary observer) can be obtained as:
vbB = vb + vB = 9 + 4 = 13 km/h
(b) Since the boy is running in the direction opposite to the direction of the motion of the belt, his speed (as observed by the stationary observer) can be obtained as:
vbB = vb + (– vB) = 9 – 4 = 5 km/h
(c) Distance between the child’s parents = 50 m
As both parents are standing on the moving belt, the speed of the child in either direction as observed by the parents will remain the same i.e., 9 km/h = 2.5 m/s.
Hence, the time taken by the child to move towards one of his parents is `50/2.5 = 20 s`
(d) If the motion is viewed by any one of the parents, answers obtained in (a) and (b) get altered. This is because the child and his parents are standing on the same belt and hence, are equally affected by the motion of the belt. Therefore, for both parents (irrespective of the direction of motion) the speed of the child remains the same i.e., 9 km/h.
For this reason, it can be concluded that the time taken by the child to reach any one of his parents remains unaltered.
Solution 2
Speed of child with respect to belt = 9 km h-1Speed of belt = 4 km h-1
(a) When the child runs in the direction of motion of the belt, then speed of child w.r.t. stationary observer = (9 + 4) km h-1 = 13 km h-1.
(b) When the child runs opposite to the direction of motion of the belt, then speed of child w.r.t. stationary observer = (9 – 4) km h-1 = 5 km h-1
(c) Speed of child w.r.t . either parent=9 km h-1
Distance to be covered = 50 m = 0.05 km 0.05 km
Time=0.05 km/9k h-1=0.0056 h =20 S
If the motion is viewed by one of the parents, then the answers to (a) and (b)are altered but answer to (c) remains unaltered.
APPEARS IN
RELATED QUESTIONS
The given figure gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals. What are the accelerations at the points A, B, C and D?

If a particle is accelerating, it is either speeding up or speeding down. Do you agree with this statement?
Give example where the velocity is opposite in direction to the acceleration.
Give example where the velocity is perpendicular to the acceleration.
A stone is released from an elevator going up with an acceleration a. The acceleration of the stone after the release is
The accelerations of a particle as seen from two frames S1 and S2 have equal magnitude 4 m/s2.
An object having a velocity 4.0 m/s is accelerated at the rate of 1.2 m/s2 for 5.0 s. Find the distance travelled during the period of acceleration.
The displacement of particle is given by x = `2/lambda (1 - e^(-lambdat))`, the acceleration of particle at 2s when λ = 2s–1 will be (Take `l`n 0.018 = – 4)
Give example of a motion where x > 0, v < 0, a > 0 at a particular instant.
An object falling through a fluid is observed to have acceleration given by a = g – bv where g = gravitational acceleration and b is constant. After a long time of release, it is observed to fall with constant speed. What must be the value of constant speed?
