Advertisements
Advertisements
Question
f(x) = 4x4 − 3x3 − 2x2 + x − 7, g(x) = x − 1
Advertisements
Solution
Let us denote the given polynomials as
`f (x) = 4x^4 - 3x^3 - 2x^2 + x - 7`
`g(x) = x-1`
We have to find the remainder when f(x) is divided byg(x).
By the remainder theorem, when f(x) is divided by g(x) the remainder is
`f(1) = 4(1)^4 - 3(1)^3 - 2(1)^2 + 1-7`
` = 4 - 3- 2 + 1- 7`
` = -7`
Now we will show remainder by actual division
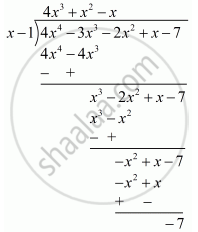
So the remainder by actual division is −7
APPEARS IN
RELATED QUESTIONS
Identify constant, linear, quadratic and cubic polynomials from the following polynomials
`p(x)=2x^2-x+4`
Verify whether the indicated numbers is zeros of the polynomials corresponding to them in the following case:
\[p(x) = x^3 - 6 x^2 + 11x - 6, x = 1, 2, 3\]
If x − 2 is a factor of the following two polynomials, find the values of a in each case x5 − 3x4 − ax3 + 3ax2 + 2ax + 4.
x3 − 10x2 − 53x − 42
x3 − 3x2 − 9x − 5
2y3 + y2 − 2y − 1
Mark the correct alternative in each of the following:
If x − 2 is a factor of x2 + 3ax − 2a, then a =
If x − 3 is a factor of x2 − ax − 15, then a =
Factorise the following:
9 – 18x + 8x2
Factorise the following:
8m3 – 2m2n – 15mn2
