Advertisements
Advertisements
प्रश्न
f(x) = 4x4 − 3x3 − 2x2 + x − 7, g(x) = x − 1
उत्तर
Let us denote the given polynomials as
`f (x) = 4x^4 - 3x^3 - 2x^2 + x - 7`
`g(x) = x-1`
We have to find the remainder when f(x) is divided byg(x).
By the remainder theorem, when f(x) is divided by g(x) the remainder is
`f(1) = 4(1)^4 - 3(1)^3 - 2(1)^2 + 1-7`
` = 4 - 3- 2 + 1- 7`
` = -7`
Now we will show remainder by actual division
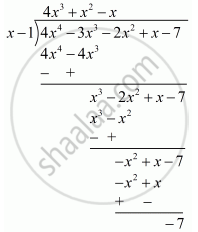
So the remainder by actual division is −7
APPEARS IN
संबंधित प्रश्न
Write the degrees of the following polynomials:
`12-x+2x^3`
Identify polynomials in the following:
`q(x)=2x^2-3x+4/x+2`
If `f(x)=2x^2-13x^2+17x+12` find `f(0)`
f(x) = x3 − 6x2 + 2x − 4, g(x) = 1 − 2x
Find the remainder when x3 + 3x2 + 3x + 1 is divided by \[x - \frac{1}{2}\].
f(x) = x5 + 3x4 − x3 − 3x2 + 5x + 15, g(x) = x + 3
x3 + 2x2 − x − 2
Let f(x) be a polynomial such that \[f\left( - \frac{1}{2} \right)\] = 0, then a factor of f(x) is
One factor of x4 + x2 − 20 is x2 + 5. The other factor is
If (x + 5) and (x – 3) are the factors of ax2 + bx + c, then values of a, b and c are
