Advertisements
Advertisements
प्रश्न
One factor of x4 + x2 − 20 is x2 + 5. The other factor is
विकल्प
x2 − 4
x − 4
x2 − 5
x + 2
उत्तर
It is given that `x^ + 5`is a factor of the polynomial
`f(x)^2 = x^4 + x^2 - 20 .`
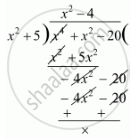
Here, reminder is zero. Therefore,` x^2 - 4` is a factor of polynomial.
APPEARS IN
संबंधित प्रश्न
Identify polynomials in the following:
`p(x)=2/3x^3-7/4x+9`
The polynomials ax3 + 3x2 − 3 and 2x3 − 5x + a when divided by (x − 4) leave the remainders R1 and R2 respectively. Find the value of the following case, if R1 = R2.
f(x) = x3 − 6x2 + 11x − 6, g(x) = x2 − 3x + 2
In the following two polynomials, find the value of a, if x + a is a factor x3 + ax2 − 2x +a + 4.
What must be subtracted from x3 − 6x2 − 15x + 80 so that the result is exactly divisible by x2 + x − 12?
2y3 − 5y2 − 19y + 42
Factorize of the following polynomials:
x3 + 13x2 + 31x − 45 given that x + 9 is a factor
If f(x) = x4 − 2x3 + 3x2 − ax − b when divided by x − 1, the remainder is 6, then find the value of a + b
When x3 − 2x2 + ax − b is divided by x2 − 2x − 3, the remainder is x − 6. The values of a and b are respectively
Factorise:
3x3 – x2 – 3x + 1
