Advertisements
Advertisements
Question
One factor of x4 + x2 − 20 is x2 + 5. The other factor is
Options
x2 − 4
x − 4
x2 − 5
x + 2
Solution
It is given that `x^ + 5`is a factor of the polynomial
`f(x)^2 = x^4 + x^2 - 20 .`
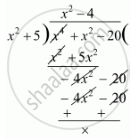
Here, reminder is zero. Therefore,` x^2 - 4` is a factor of polynomial.
APPEARS IN
RELATED QUESTIONS
Identify polynomials in the following:
`p(x)=2/3x^3-7/4x+9`
Identify constant, linear, quadratic and cubic polynomials from the following polynomials
`p(x)=2x^2-x+4`
Using factor theorem, factorize each of the following polynomials:
x3 + 6x2 + 11x + 6
If \[x = \frac{1}{2}\] is a zero of the polynomial f(x) = 8x3 + ax2 − 4x + 2, find the value of a.
If both x − 2 and \[x - \frac{1}{2}\] are factors of px2 + 5x + r, then
Factorise the following:
x² + 10x + 24
Factorise the following:
p² – 6p – 16
Factorise the following:
y2 – 16y – 80
Factorise the following:
8m3 – 2m2n – 15mn2
Factorise:
2x3 – 3x2 – 17x + 30
