Question

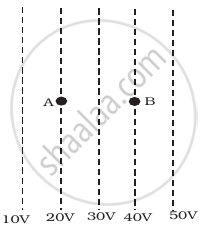
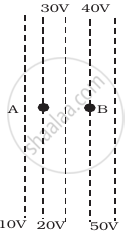
Figure shows some equipotential lines distributed in space. A charged object is moved from point A to point B.

(i)	(ii)	(iii)

Options

• The work done in figure (i) is the greatest.

• The work done in figure (ii) is least.

• The work done is the same in figure (i), (ii) and (iii).

• The work done in figure (iii) is greater than figure (ii) but equal to that in figure (i).

Answer 1

The work done is the same in figure (i), (ii) and (iii).

Explanation:

For a given charge distribution, locus of all points or regions for which the electric potential has a constant value are called equipotential regions. Such equipotential can be surfaces, volumes or lines.

Regarding equipotential surface the following points should be kept in mind:

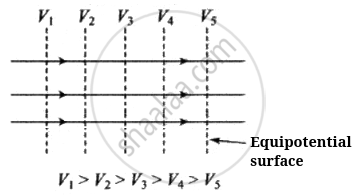
• The density of the equipotential lines gives an idea about the magnitude of the electric field. Higher the density, larger the field strength.
• The direction of the electric field is perpendicular to the equipotential surfaces or lines.

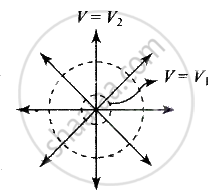
Spherical equipotential surface

• The equipotential surfaces produced by a point charge or a spherically charge distribution are a family of concentric spheres.
• For a uniform electric field, the equipotential surfaces are a family of plane perpendicular to the field lines.
• A metallic surface of any shape is an equipotential surface.
• Equipotential surfaces can never cross each other.
• The work done in moving a charge along an equipotential surface is always zero.

As the director of the electric field is always perpendicular to one equipotential surface maintained at high electrostatic potential than another equipotential surface maintained at low electrostatic potential. Hence the direction of electric field is from B to A in all three cases.

The positively charged particle experiences electrostatic force along the direction of the electric field, hence moves in the direction opposite to the electric field. Thus, the work done by the electric field on the charge will be negative. We know

`W_("electrical") = -ΔU = -qΔV = q(V_("initial") – V_("final"))`

Here initial and final potentials are same in all three cases and same charge is moved, so work done is same in all three cases.