Advertisements
Advertisements
Question
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2 × 10−9 C from a point P (0, 0, 3 cm) to a point Q (0, 4 cm, 0), via a point R (0, 6 cm, 9 cm).
Solution
Charge located at the origin, q = 8 mC = 8 × 10−3 C
Magnitude of a small charge, which is taken from a point P to point R to point Q, q1 = −2 × 10−9 C
All the points are represented in the given figure.
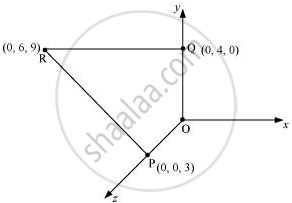
Point P is at a distance, d1 = 3 cm, from the origin along the z-axis.
Point Q is at a distance, d2 = 4 cm, from the origin along the y-axis.
Potential at point P, `"V"_1 = "q"/(4piin_0 xx "d"_1)`
Potential at point Q,`"V"_2 = "q"/(4piin_0 xx "d"_2)`
Work done (W) by the electrostatic force is independent of the path.
∴ `"W" = "q"_1 ["V"_2 - "V"_1]`
= `"q"_1["q"/(4piin_0"d"_2) - "q"/(4piin_0"d"_1)]`
= `("qq"_1)/(4piin_0) [1/"d"_2 - 1/"d"_1]` .......(1)
Where, `1/(4piin_0) = 9 xx 10^9 "N m"^2 "C"^-2`
∴ `"W" = 9 xx 10^9 xx 8 xx 10^-3 xx (-2 xx 10^-9)[1/0.04 - 1/0.03]`
= `-144 xx 10^-3 xx ((-25)/3)`
= 1.27 J
Therefore, work done during the process is 1.27 J.
APPEARS IN
RELATED QUESTIONS
Figure shows a charge array known as an electric quadrupole. For a point on the axis of the quadrupole, obtain the dependence of potential on r for r/a >> 1, and contrast your results with that due to an electric dipole, and an electric monopole (i.e., a single charge).

Work done by a uniform electric field 'E' in moving a charge 'q' at a distance 'd' from a to b is ______.
Figure shows some equipotential lines distributed in space. A charged object is moved from point A to point B.
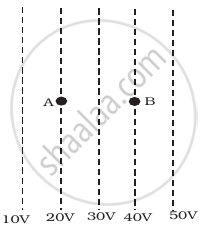 |
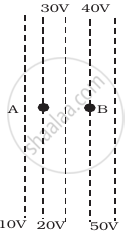 |
 |
| (i) | (ii) | (iii) |
Depict the orientation of an electric dipole in (a) stable and (b) unstable equilibrium in an external uniform electric field. Write the potential energy of the dipole in each case.
