Advertisements
Advertisements
Question
A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
Solution
Length of the side of a cube = b
Charge at each of its vertices = q
A cube of side b is shown in the following figure.

d = Diagonal of one of the six faces of the cube
`"d"^2 = sqrt("b"^2 + "b"^2) = sqrt(2"b"^2)`
`"d" = "b"sqrt2`
l = Length of the diagonal of the cube
`"l"^2 = sqrt("d"^2 + "b"^2)`
= `sqrt((sqrt(2)"b")^2) + "b"^2`
= `sqrt(2"b"^2 + "b"^2)`
= `sqrt(3"b"^2)`
`"l" = "b"sqrt3`
`"r" = 1/2 = ("b"sqrt3)/2` is the distance between the center of the cube and one of the eight vertices.
The electric potential (V) at the centre of the cube is due to the presence of eight charges at the vertices.
`"V" = (8"q")/(4piin_0)`
= `(8"q")/(4piin_0("b"sqrt3/2))`
= `(4"q")/(sqrt3 pi in_0 "b")`
Therefore, the potential at the centre of the cube is `(4"q")/(sqrt3 pi in_0 "b")`.
The electric field at the centre of the cube, due to the eight charges, gets cancelled. This is because the charges are distributed symmetrically with respect to the centre of the cube. Hence, the electric field is zero at the centre.
APPEARS IN
RELATED QUESTIONS
If one of the two electrons of a H2 molecule is removed, we get a hydrogen molecular ion `"H"_2^+`. In the ground state of an `"H"_2^+`, the two protons are separated by roughly 1.5 Å, and the electron is roughly 1 Å from each proton. Determine the potential energy of the system. Specify your choice of zero potential energy.
Four point charges Q, q, Q and q are placed at the corners of a square of side 'a' as shown in the figure.
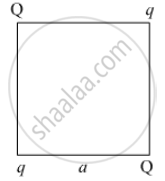
Find the
1) resultant electric force on a charge Q, and
2) potential energy of this system.
Find out the amount of the work done to separate the charges at infinite distance.
If a charge q0 is there in an electric field caused by several point charges qi. The potential energy of q0 is given by ________.
The work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential at that point is ______.
- Assertion (A): An electron has a high potential energy when it is at a location associated with a more negative value of potential, and a low potential energy when at a location associated with a more positive potential.
- Reason (R): Electrons move from a region of higher potential to region of lower potential.
Select the most appropriate answer from the options given below:
Calculate potential energy of a point charge – q placed along the axis due to a charge +Q uniformly distributed along a ring of radius R. Sketch P.E. as a function of axial distance z from the centre of the ring. Looking at graph, can you see what would happen if – q is displaced slightly from the centre of the ring (along the axis)?
- In a quark model of elementary particles, a neutron is made of one up quarks [charge (2/3) e] and two down quarks [charges –(1/3) e]. Assume that they have a triangle configuration with side length of the order of 10–15 m. Calculate electrostatic potential energy of neutron and compare it with its mass 939 MeV.
- Repeat above exercise for a proton which is made of two up and one down quark.
Justify your answers for each case.
State the significance of the negative value of electrostatic potential energy of a system of charges.
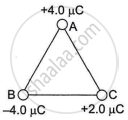
Three charges are placed at the corners of an equilateral triangle ABC of side 2.0 m as shown in the figure. Calculate the electric potential energy of the system of three charges.
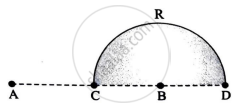
Charges (+q) and (–q) are placed at points A and B respectively which are a distance 2L apart. C is the midpoint between A and B. What is the work done in moving a charge +Q along the semicircle CRD?