Advertisements
Advertisements
Question
Fill in the following blank with a suitable word:
When a ray of light goes from air into a clear material, you see the ray bend. How much the ray bends is determined by the ............... of the material.
Solution
When a ray of light goes from air into a clear material, you see the ray bend. How much the ray bends is determined by therefractive index of the material.
APPEARS IN
RELATED QUESTIONS
The absolute refractive indices of two media 'A' and 'B' are 2.0 and 1.5 respectively. If the speed of light in medium 'B' is 2 × 108 m/s, calculate the speed of light in:
(i) vacuum,
(ii) medium 'A'.
You are given kerosene, turpentine and water. In which of these does the light travel fastest? Use the information given in Table.
| Material medium |
Refractive index | Material medium | Refractive index |
| Air | 1.0003 | Canada Balsam | 1.53 |
| Ice | 1.31 | – | – |
| Water | 1.33 | Rock salt | 1.54 |
| Alcohol | 1.36 | – | – |
| Kerosene | 1.44 | Carbon disulphide | 1.63 |
| Fused quartz |
1.46 | Dense flint glass |
1.65 |
| Turpentine oil | 1.47 | Ruby | 1.71 |
| Benzene | 1.50 | Sapphire | 1.77 |
| Crown glass |
1.52 | Diamond | 2.42 |
The speed of light in air is:
(a) 3 × 108 cm/s
(b) 3 × 108 mm/s
(c) 3 × 108 km/s
(d) 3 × 108 m/s
The refractive index of diamond is 2.42. What is the meaning of this statement in relation to the speed of light?
Name a liquid whose mass density is less than that of water but it is optically denser than water.
The velocity of light in a vacuum is 3 x 108 ms-1 and in glass is 2 x 108 ms-1. The refractive index of glass is ______.
Match the Columns:
| Column ‘A’ | Column ‘B’ |
| Refractive index of water | (a) 1.31 |
| (b) 1.36 | |
| (c) 1.33 |
What happens when a light ray passes from a rarer medium to a denser medium?
Match the pair:
| Group 'A' | Group 'B' | |
| Substance | Refractive index | |
| Air | (a) | 1.33 |
| (b) | 1.46 | |
| (c) | 1.0003 |
A light ray enters from medium A to medium B as shown in the figure.
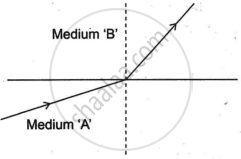
If the speed of light in medium A is `v_a` and in medium B is `v_b`, what is the refractive index of B with respect to A.
