Advertisements
Advertisements
Question
Find the area of the triangle formed by the lines joining the vertex of the parabola x2 = 12y to the ends of its latus rectum.
Solution
The given parabola is x2 = 12y.
On comparing this equation with x2 = 4ay, we obtain 4a = 12 ⇒ a = 3
∴ The coordinates of foci are S (0, a) = S (0, 3)
Let AB be the latus rectum of the given parabola.
The given parabola can be roughly drawn as
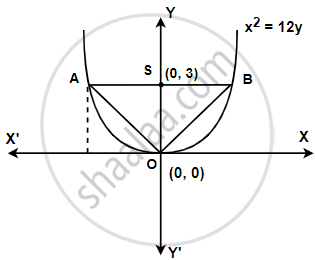
At y = 3, x2 = 12 (3) ⇒ x2 = 36 ⇒ x = ±6
∴ The coordinates of A are (–6, 3), while the coordinates of B are (6, 3).
Therefore, the vertices of ΔOAB are O (0, 0), A (–6, 3), and B (6, 3).
Area of Δ OAB = `1/2 |0(3 - 3) + (-6) (3 - 0) + 6 (0 - 3)|"unit"^2`
= `1/2 |(-6) (3) + 6(-3)| "unit"^2`
= `1/2 |-18 - 18| "unit"^2`
= `1/2 |-36| "unit"^2`
= `1/2 xx 36 "unit"^2`
= 18 unit2
Thus, the required area of the triangle is 18 unit2.
APPEARS IN
RELATED QUESTIONS
Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum.
y2 = 12x
Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum.
x2 = – 16y
Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum.
x2 = –9y
Find the area of the triangle formed by the lines joining the vertex of the parabola \[x^2 = 12y\] to the ends of its latus rectum.
Find the coordinates of the point of intersection of the axis and the directrix of the parabola whose focus is (3, 3) and directrix is 3x − 4y = 2. Find also the length of the latus-rectum.
If b and c are lengths of the segments of any focal chord of the parabola y2 = 4ax, then write the length of its latus-rectum.
If the parabola y2 = 4ax passes through the point (3, 2), then find the length of its latus rectum.
The vertex of the parabola (y + a)2 = 8a (x − a) is
If the focus of a parabola is (−2, 1) and the directrix has the equation x + y = 3, then its vertex is
The length of the latus-rectum of the parabola y2 + 8x − 2y + 17 = 0 is
The length of the latus-rectum of the parabola 4y2 + 2x − 20y + 17 = 0 is
The focus of the parabola y = 2x2 + x is
Which of the following points lie on the parabola x2 = 4ay?
If the equation of the parabola is x2 = – 8y, find coordinates of the focus, the equation of the directrix and length of latus rectum.
If the latus rectum of an ellipse with axis along x-axis and centre at origin is 10, distance between foci = length of minor axis, then the equation of the ellipse is ______.
If the eccentricity of an ellipse is `5/8` and the distance between its foci is 10, then find latus rectum of the ellipse.
If the parabola y2 = 4ax passes through the point (3, 2), then the length of its latus rectum is ______.
The length of the latus rectum of the ellipse 3x2 + y2 = 12 is ______.
