Question

If P (2, – 1), Q(3, 4), R(–2, 3) and S(–3, –2) be four points in a plane, show that PQRS is a rhombus but not a square. Find the area of the rhombus

Answer 1

The given points are P(2, –1), Q(3, 4), R(–2, 3) and S(–3, –2).
We have,

`PQ=sqrt((3-2)^{2}+(4+1)^{2})=sqrt(1^{2}+5^{2})=\sqrt{26`

`QR=sqrt((-2-3)^{2}+(3-4)^{2})=\sqrt{25+1}=\sqrt{26}`

`RS=sqrt((-3+2)^{2}+(-2-3)^{2})=\sqrt{1+25}=\sqrt{26}" units"`

`SP=sqrt((-3-2)^{2}+(-2+1)^{2})=\sqrt{25+1}=\sqrt{26}" units"`

`PR=sqrt((-2-2)^{2}+(3+1)^{2})=\sqrt{16+16}=4\sqrt{2}" units"`

`QS=sqrt((-3-3)^{2}+(-2-4)^{2})=\sqrt{36+36}=6\sqrt{2}" units"`

∴ PQ = QR = RS = SP = units and, PR ≠ QS

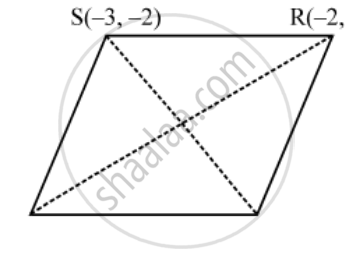
This means that PQRS is a quadrilateral whose sides are equal but diagonals are not equal.

Thus, PQRS is a rhombus but not a square.

Now, Area of rhombus `PQRS = \frac { 1 }{ 2 } × ("Product of lengths of diagonals")`

⇒ Area of rhombus `PQRS = \frac { 1 }{ 2 } × (PR × QS)`

⇒ Area of rhombus PQRS `=( \frac{1}{2}\times 4\sqrt{2}\times 6\sqrt{2})sq.units=24sq.units`