Advertisements
Advertisements
Question
Find the coordinates of the centre of the circle passing through the points (0, 0), (–2, 1) and (–3, 2). Also, find its radius.
Sum
Solution
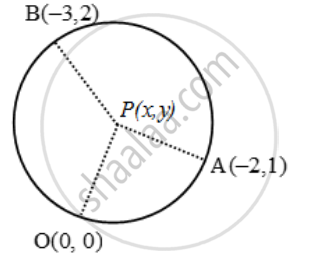
Let P (x, y) be the centre of the circle passing through the points O(0, 0), A(–2,1) and B(–3,2).
Then, OP = AP = BP
Now,
`OP = AP ⇒ OP^2 = AP^2`
`⇒ x^2 + y^2 = (x + 2)^2 + (y – 1)^2`
`⇒ x^2 + y^2 = x^2 + y^2 + 4x – 2y + 5`
⇒ 4x – 2y + 5 = 0 ….(1)
and, OP = BP ⇒ OP2 = BP2
`⇒ x^2 + y^2 = (x + 3)^2 + (y – 2)^2`
`⇒ x^2 + y^2 = x^2 + y^2 + 6x – 4y + 13`
⇒ 6x – 4y + 13 = 0 ….(2)
On solving equations (1) and (2), we get
`x = \frac { 3 }{ 2 } and y = \frac { 11 }{ 2 }`
Thus, the coordinates of the centre are `( \frac{3}{2},\frac{11}{2})`
Now, `\text{}Radius=OP=sqrt(x^{2}+y^{2})=\sqrt{\frac{9}{4}+\frac{121}{4}}`
`=\frac{1}{2}\sqrt{130}`
shaalaa.com
Is there an error in this question or solution?
