Advertisements
Advertisements
Question
Find the current through the 10 Ω resistor shown in the figure.
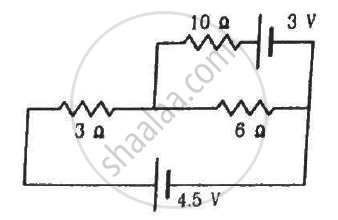
Sum
Solution
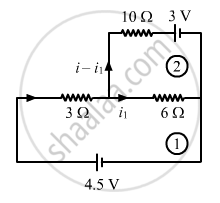
Applying KVL in loop 1, we get:-
3i + 6i1 = 4.5 ...............(1)
Applying KVL in loop 2, we get:-
\[\left( i - i_1 \right)10 + 3 - 6 i_1 = 0\]
\[10i - 16 i_1 = - 3 ..............(2)\]
Multiplying equation (1) by 10 and (2) by 3 and then, subtracting (2) from (1), we get:-
\[- 108 i_1 = - 54\]
\[ \Rightarrow i_1 = \frac{54}{108} = \frac{1}{2} = 0 . 5\]
Substituting the value of i1 in (1), we get:-
\[3i + 6 \times \frac{1}{2} - 4 . 5 = 0\]
\[3i - 1 . 5 = 0\]
\[ \Rightarrow i = \frac{1 . 5}{3} = 0 . 5\]
So, current flowing through the 10 Ω resistor = i - i1 = 0.5 - 0.5 = 0 A
shaalaa.com
Is there an error in this question or solution?
