Advertisements
Advertisements
Question
Find the circuit in the three resistors shown in the figure.
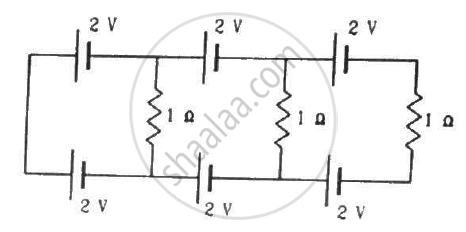
Solution
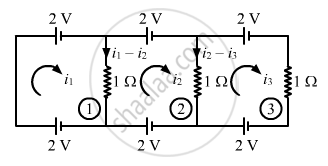
Applying KVL in loop 1, we get:-
\[2 + \left( i_1 - i_2 \right) \times 1 - 2 = 0\]
\[ \Rightarrow i_1 = i_2\]
Applying KVL in loop 2, we get:-
\[2 + \left( i_2 - i_3 \right) \times 1 - 2 - \left( i_1 - i_2 \right) \times 1 = 0\]
\[ \Rightarrow i_2 - i_3 - i_1 + i_2 = 0\]
\[ i_1 = i_2 \]
\[ \Rightarrow i_2 - i_3 - i_2 + i_2 = 0\]
\[ \Rightarrow i_2 = i_3\]
Applying KVL in loop 3, we get:-
\[2 + i_3 - 2 - \left( i_2 - i_3 \right) = 0\]
\[ \Rightarrow i_3 = 0\]
\[ i_1 = i_2 = i_3 \]
\[ \therefore i_1 = i_2 = i_3 = 0\]
APPEARS IN
RELATED QUESTIONS
Kirchhoff's junction law is equivalent to .............................
(a) conservation of energy.
(b) conservation of charge
(c) conservation of electric potential
(d) conservation of electric flux
State the two Kirchhoff’s rules used in electric networks. How are there rules justified?
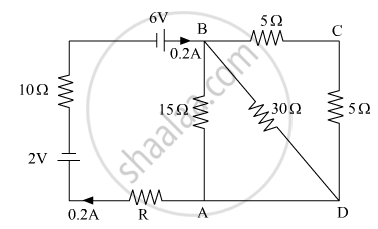
Calculate the value of the resistance R in the circuit shown in the figure so that the current in the circuit is 0.2 A. What would b the potential difference between points A and B?
In the given circuit, assuming point A to be at zero potential, use Kirchhoff’s rules to determine the potential at point B.

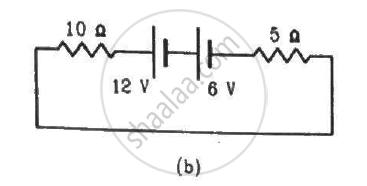
Consider the circuit shown in the figure. Find (a) the current in the circuit (b) the potential drop across the 5 Ω resistor (c) the potential drop across the 10 Ω resistor (d) Answer the parts (a), (b) and (c) with reference to the figure.
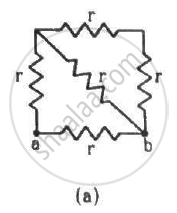
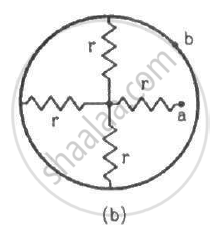
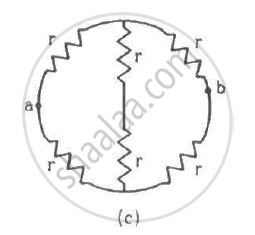
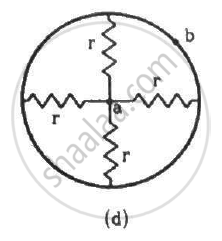
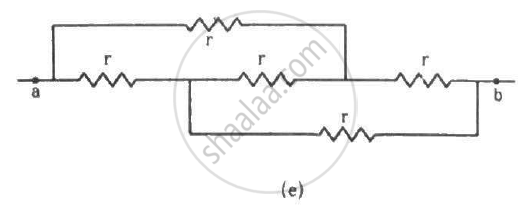
Find the equivalent resistances of the networks shown in the figure between the points a and b.
An infinite ladder is constructed with 1 Ω and 2 Ω resistors, as shown in the figure. (a) Find the effective resistance between the points A and B. (b) Find the current that passes through the 2 Ω resistor nearest to the battery.

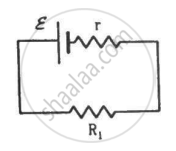
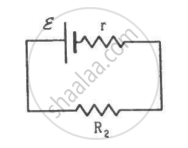
Two unequal resistances, R1 and R2, are connected across two identical batteries of emf ε and internal resistance r (see the figure). Can the thermal energies developed in R1 and R2 be equal in a given time? If yes, what will be the condition?
Solve the following question.
Using Kirchhoff’s rules, calculate the current through the 40 Ω and 20 Ω resistors in the following circuit.

State and explain Kirchhoff’s rules.
A copper wire of 10-6 m2 area of cross-section, carries a current of 2 A. If the number of electrons per cubic meter is 8 × 1028, calculate the current density and average drift velocity.
Kirchhoff’s second law is a consequence of law of conservation of ______.
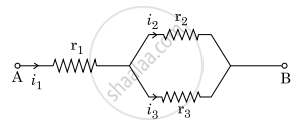
Three resistors having resistances r1, r2 and r3 are connected as shown in the given circuit. The ratio `"i"_3/"i"_1` of currents in terms of resistances used in the circuit is :
Kirchhoff’s junction rule is a reflection of ______.
- conservation of current density vector.
- conservation of charge.
- the fact that the momentum with which a charged particle approaches a junction is unchanged (as a vector) as the charged particle leaves the junction.
- the fact that there is no accumulation of charges at a junction.
Why are alloys used for making standard resistance coils?
Derive the equation of the balanced state in a Wheatstone bridge using Kirchhoff’s laws.
A 6-volt battery is connected to the terminals of a three-metre-long wire of uniform thickness and resistance of 100 ohms. The difference of potential between two points on the wire separated by a distance of 50 cm will be ______.
The figure below shows two batteries, E1 and E2, having emfs of 18V and 10V and internal resistances of 1 Ω and 2 Ω, respectively. W1, W2 and W3 are uniform metallic wires AC, FD and BE having resistances of 8 Ω, 6 Ω and 10 Ω respectively. B and E are midpoints of the wires W1 and W2. Using Kirchhoff's laws of electrical circuits, calculate the current flowing in the wire W3:

