Advertisements
Advertisements
Questions
State the two Kirchhoff’s rules used in electric networks. How are there rules justified?
State Kirchhoff's rules. Explain briefly how these rules are justified.
Solution 1
Kirchhoff’s first rule:
In any electrical network, the algebraic sum of currents meeting at a junction is always zero.
∑I=0
In the junction below, let I1, I2, I3, I4 and I5 be the current in the conductors with directions as shown in the figure below. I5 and I3 are the currents which enter and currents I1, I2 and I4 leave.
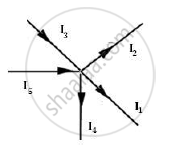
According to the Kirchhoff’s law, we have
(–I1) + (−I2) + I3 + (−I4) + I5 = 0 Or I1 + I2 + I4 = I3 + I5
Thus, at any junction of several circuit elements, the sum of currents entering the junction must equal the sum of currents leaving it. This is a consequence of charge conservation and the assumption that currents are steady, i.e. no charge piles up at the junction.
Kirchhoff’s second rule: The algebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero. or
The algebraic sum of the e.m.f. in any loop of a circuit is equal to the algebraic sum of the products of currents and resistances in it.
Mathematically, the loop rule may be expressed as ∑E = ΣIR.
Solution 2
Kirchhoff’s First Law − Junction Rule
In an electrical circuit, the algebraic sum of the currents meeting at a junction is always zero.
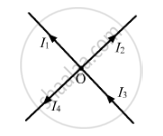
I1, I2 I3, and I4 are the currents flowing through the respective wires.
Convention:
The current flowing towards the junction is taken as positive.
The current flowing away from the junction is taken as negative.
I3 + (− I1) + (− I2) + (− I4) = 0
This law is based on the law of conservation of charge.
Kirchhoff’s Second Law − Loop Rule
In a closed loop, the algebraic sum of the emfs is equal to the algebraic sum of the products of the resistances and the currents flowing through them.
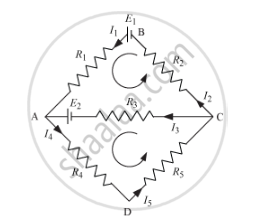
For the closed loop BACB:
E1 − E2 = I1R1 + I2R2 − I3R3
For the closed loop CADC:
E2 = I3R3 + I4R4 + I5R5
This law is based on the law of conservation of energy
APPEARS IN
RELATED QUESTIONS
Kirchhoff's junction law is equivalent to .............................
(a) conservation of energy.
(b) conservation of charge
(c) conservation of electric potential
(d) conservation of electric flux
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (11/3) Ω?
State Kirchhoff's rules for an electric network. Using Kirchhoff's rules, obtain the balance condition in terms of the resistances of four arms of Wheatstone bridge.
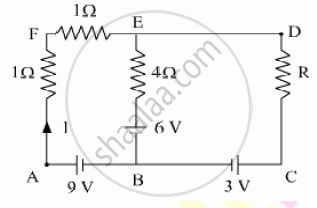
Using Kirchhoff’s rules determine the value of unknown resistance R in the circuit so that no current flows through 4 Ω resistance. Also find the potential difference between A and D.
Find the circuit in the three resistors shown in the figure.
Kirchhoff’s second law is a consequence of law of conservation of ______.
Assertion: Kirchhoff’s junction rule follows from conservation of charge.
Reason: Kirchhoff’s loop rule follows from conservation of momentum.
The Kirchhoff's second law (ΣiR = ΣE), where the symbols have their usual meanings, is based on ______.
Kirchhoff’s junction rule is a reflection of ______.
- conservation of current density vector.
- conservation of charge.
- the fact that the momentum with which a charged particle approaches a junction is unchanged (as a vector) as the charged particle leaves the junction.
- the fact that there is no accumulation of charges at a junction.
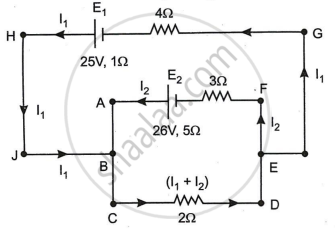
In the circuit shown in Figure below, E1 and E2 are batteries having emfs of 25V and 26V. They have an internal resistance of 1 Ω and 5 Ω respectively. Applying Kirchhoff’s laws of electrical networks, calculate the currents I1 and I2.