Advertisements
Advertisements
Question
Using Kirchhoff’s rules determine the value of unknown resistance R in the circuit so that no current flows through 4 Ω resistance. Also find the potential difference between A and D.
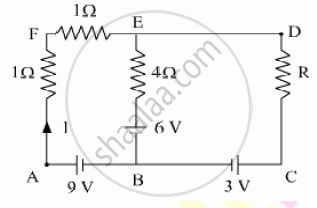
Solution
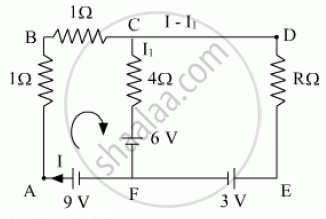
Apply Kirchhoff’s In loop ABCFA:-
I + I + 4I1 = 9 − 6
2I + 4I1 = 3 … (1)
As there is no current flowing through the 4Ω resistance,
I1 = 0
Or, 2I = 3
Or, I = 1.5A
Thus the current through resistances R is 1.5A.
As there is no current through branch CF, thus equivalent circuit will be,
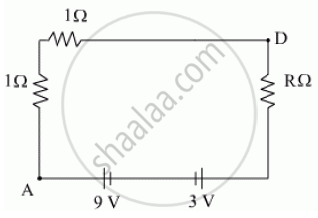
By applying Kirchhoff’s loop law we get,
1.5 + 1.5 + R (1.5) = 9 − 3
R = 2Ω
Potential difference between A and D = (9 − 3) = 6V
APPEARS IN
RELATED QUESTIONS
Kirchhoff's junction law is equivalent to .............................
(a) conservation of energy.
(b) conservation of charge
(c) conservation of electric potential
(d) conservation of electric flux
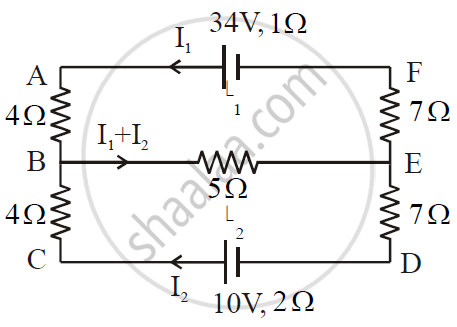
ε1 and ε2 are two batteries having emf of 34V and 10V respectively and internal resistance of 1Ω and 2Ω respectively. They are connected as shown in the figure below. Using Kirchhoff’s Laws of electrical networks, calculate the currents I1 and I2.
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (11/3) Ω?
Find the circuit in the three resistors shown in the figure.
On which conservation principle is Kirchoff's Second Law of electrical networks based?
State Kirchhoff ’s voltage rule.
Kirchhoff’s second law is a consequence of law of conservation of ______.
Assertion: Kirchhoff’s junction rule follows from conservation of charge.
Reason: Kirchhoff’s loop rule follows from conservation of momentum.
Kirchhoff’s junction rule is a reflection of ______.
- conservation of current density vector.
- conservation of charge.
- the fact that the momentum with which a charged particle approaches a junction is unchanged (as a vector) as the charged particle leaves the junction.
- the fact that there is no accumulation of charges at a junction.
