Advertisements
Advertisements
प्रश्न
State the two Kirchhoff’s rules used in electric networks. How are there rules justified?
State Kirchhoff's rules. Explain briefly how these rules are justified.
उत्तर १
Kirchhoff’s first rule:
In any electrical network, the algebraic sum of currents meeting at a junction is always zero.
∑I=0
In the junction below, let I1, I2, I3, I4 and I5 be the current in the conductors with directions as shown in the figure below. I5 and I3 are the currents which enter and currents I1, I2 and I4 leave.
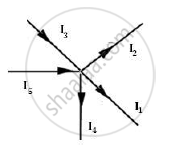
According to the Kirchhoff’s law, we have
(–I1) + (−I2) + I3 + (−I4) + I5 = 0 Or I1 + I2 + I4 = I3 + I5
Thus, at any junction of several circuit elements, the sum of currents entering the junction must equal the sum of currents leaving it. This is a consequence of charge conservation and the assumption that currents are steady, i.e. no charge piles up at the junction.
Kirchhoff’s second rule: The algebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero. or
The algebraic sum of the e.m.f. in any loop of a circuit is equal to the algebraic sum of the products of currents and resistances in it.
Mathematically, the loop rule may be expressed as ∑E = ΣIR.
उत्तर २
Kirchhoff’s First Law − Junction Rule
In an electrical circuit, the algebraic sum of the currents meeting at a junction is always zero.
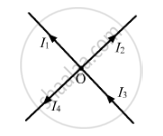
I1, I2 I3, and I4 are the currents flowing through the respective wires.
Convention:
The current flowing towards the junction is taken as positive.
The current flowing away from the junction is taken as negative.
I3 + (− I1) + (− I2) + (− I4) = 0
This law is based on the law of conservation of charge.
Kirchhoff’s Second Law − Loop Rule
In a closed loop, the algebraic sum of the emfs is equal to the algebraic sum of the products of the resistances and the currents flowing through them.
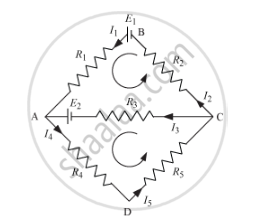
For the closed loop BACB:
E1 − E2 = I1R1 + I2R2 − I3R3
For the closed loop CADC:
E2 = I3R3 + I4R4 + I5R5
This law is based on the law of conservation of energy
APPEARS IN
संबंधित प्रश्न
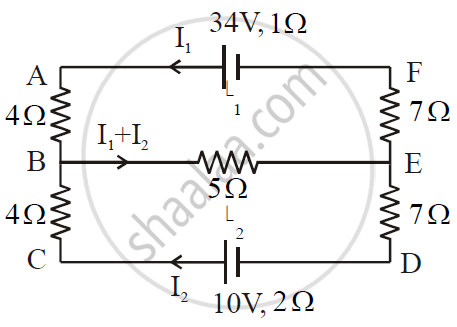
ε1 and ε2 are two batteries having emf of 34V and 10V respectively and internal resistance of 1Ω and 2Ω respectively. They are connected as shown in the figure below. Using Kirchhoff’s Laws of electrical networks, calculate the currents I1 and I2.
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (11/3) Ω?
Determine the equivalent resistance of networks shown in Fig.
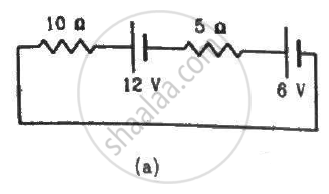
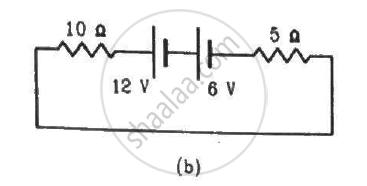
Consider the circuit shown in the figure. Find (a) the current in the circuit (b) the potential drop across the 5 Ω resistor (c) the potential drop across the 10 Ω resistor (d) Answer the parts (a), (b) and (c) with reference to the figure.
Twelve wires, each of equal resistance r, are joined to form a cube, as shown in the figure. Find the equivalent resistance between the diagonally-opposite points a and f.

Obtain the condition for bridge balance in Wheatstone’s bridge.
A potentiometer wire has a length of 4 m and resistance of 20 Ω. It is connected in series with resistance of 2980 Ω and a cell of emf 4 V. Calculate the potential along the wire.
Power P is to be delivered to a device via transmission cables having resistance RC. If V is the voltage across R and I the current through it, find the power wasted and how can it be reduced.
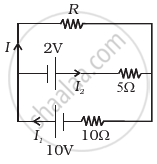
Two cells of voltage 10V and 2V and internal resistances 10Ω and 5Ω respectively, are connected in parallel with the positive end of 10V battery connected to negative pole of 2V battery (Figure). Find the effective voltage and effective resistance of the combination.
A 6-volt battery is connected to the terminals of a three-metre-long wire of uniform thickness and resistance of 100 ohms. The difference of potential between two points on the wire separated by a distance of 50 cm will be ______.
