Advertisements
Advertisements
प्रश्न
A potentiometer wire has a length of 4 m and resistance of 20 Ω. It is connected in series with resistance of 2980 Ω and a cell of emf 4 V. Calculate the potential along the wire.
उत्तर
Given data:
l = 4m of R = 20Ω
In series with R’ = 2980Ω
E = 4 V
Since 20 is in series with 2980
Reff = 20 + 2980 = 3000
current I = `"V"/"R"_"eff" = 4/3000 = 1.3 xx 10^-3 "A"`
I = `1.3 xx 10^-3`A
Potential along the wire of 4 m length is,
`"V"/"l" - "IR"/"l" = (1.3 xx 10^-3 xx 20)/4`
`= (26 xx 10^-3)/4`
= 6.5 × 10-3 Vm-1
`"V"/"l" = 6.5 xx 10^-2 "Vm"^-1`
Potential = `0.65 xx 10^-2 "Vm"^-1`
APPEARS IN
संबंधित प्रश्न
Use Kirchhoff's rules to obtain conditions for the balance condition in a Wheatstone bridge.
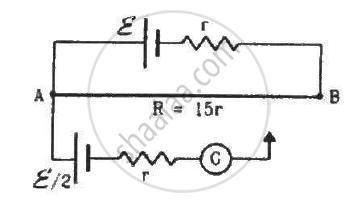
Calculate the value of the resistance R in the circuit shown in the figure so that the current in the circuit is 0.2 A. What would b the potential difference between points A and B?
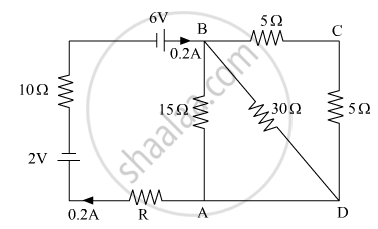
In the given circuit, assuming point A to be at zero potential, use Kirchhoff’s rules to determine the potential at point B.

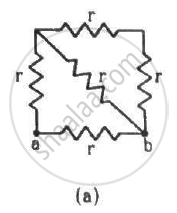
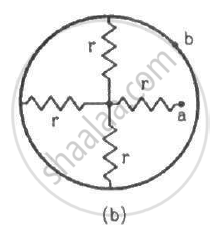
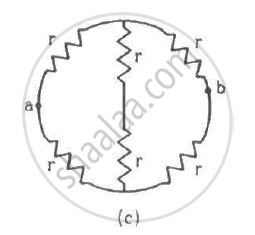
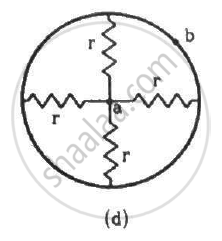
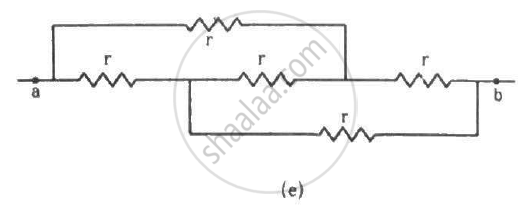
Find the equivalent resistances of the networks shown in the figure between the points a and b.
An infinite ladder is constructed with 1 Ω and 2 Ω resistors, as shown in the figure. (a) Find the effective resistance between the points A and B. (b) Find the current that passes through the 2 Ω resistor nearest to the battery.

Consider the potentiometer circuit as arranged in the figure. The potentiometer wire is 600 cm long. (a) At what distance from the point A should the jockey touch the wire to get zero deflection in the galvanometer? (b) If the jockey touches the wire at a distance of 560 cm from A, what will be the current in the galvanometer?
On which conservation principle is Kirchoff's Second Law of electrical networks based?
A copper wire of 10-6 m2 area of cross-section, carries a current of 2 A. If the number of electrons per cubic meter is 8 × 1028, calculate the current density and average drift velocity.
Three resistors having resistances r1, r2 and r3 are connected as shown in the given circuit. The ratio `i_3/i_1` of currents in terms of resistances used in the circuit is: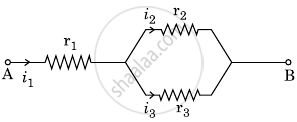
The figure below shows two batteries, E1 and E2, having emfs of 18V and 10V and internal resistances of 1 Ω and 2 Ω, respectively. W1, W2 and W3 are uniform metallic wires AC, FD and BE having resistances of 8 Ω, 6 Ω and 10 Ω respectively. B and E are midpoints of the wires W1 and W2. Using Kirchhoff's laws of electrical circuits, calculate the current flowing in the wire W3:

