Advertisements
Advertisements
प्रश्न
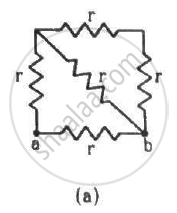
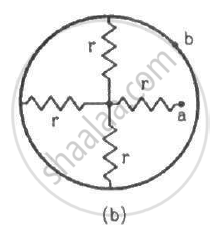
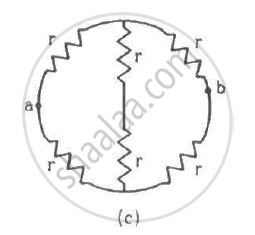
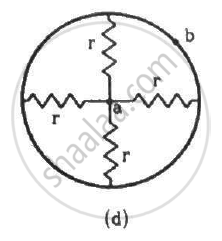
Find the equivalent resistances of the networks shown in the figure between the points a and b.
उत्तर
(a) The circuit can be simplified stepwise, as shown below.
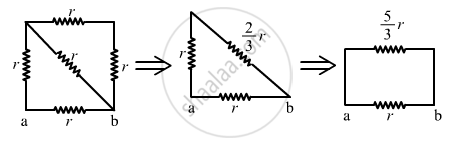
The effective resistance between the points a and b,
\[R_{eff} = \frac{\frac{5r}{3} \times r}{\frac{5r}{3} + r} = \frac{5r}{8}\]
(b) The circuit can be simplified, as shown below.
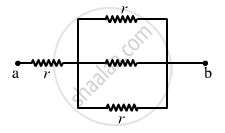
The effective resistance between the points a and b,
\[R_{eff} = \left( \frac{r}{3} \right) + r = \frac{4r}{3}\]
(c)
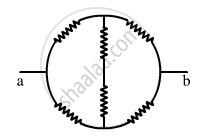
From the figure, it can be seen that axbya is a balanced Wheatstone bridge. The resistors in branch xy will, thus, become ineffective. The circuit can be simplified as under
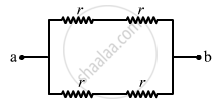
The effective resistance between the points a and b,
\[R_{eff} = \left( \frac{2r \times 2r}{2r + 2r} \right) = r\]
(d) The circuit can be simplified as shown below.
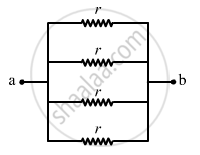
The effective resistance between the points a and b,
\[R_{eff} = \frac{r}{4}\]
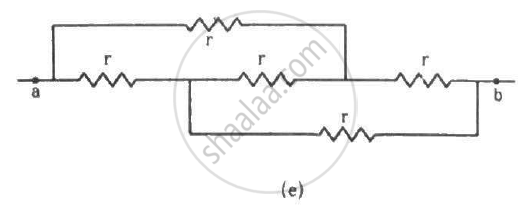
(e) The circuit can be redrawn as shown below.

Now, we can see that the circuit is a balanced Wheatstone bridge. So, the branch xy will become ineffective. Thus, the simplified circuit will become as shown below.
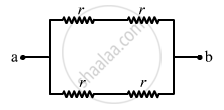
The effective resistance between the points a and b,
\[R_{eff} = \left( \frac{2r \times 2r}{2r + 2r} \right) = r\]
APPEARS IN
संबंधित प्रश्न
Use Kirchhoff's rules to obtain conditions for the balance condition in a Wheatstone bridge.
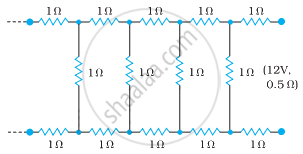
Determine the current drawn from a 12 V supply with internal resistance 0.5 Ω by the infinite network shown in the figure. Each resistor has 1 Ω resistance.
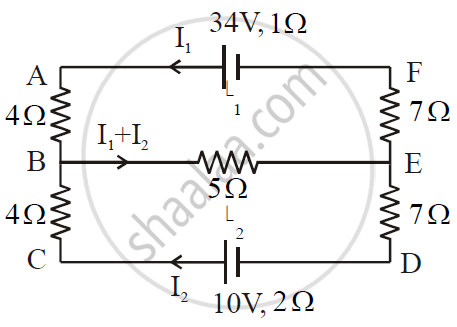
ε1 and ε2 are two batteries having emf of 34V and 10V respectively and internal resistance of 1Ω and 2Ω respectively. They are connected as shown in the figure below. Using Kirchhoff’s Laws of electrical networks, calculate the currents I1 and I2.
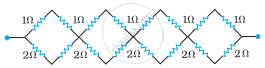
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (6/11) Ω?
Determine the equivalent resistance of networks shown in Fig.
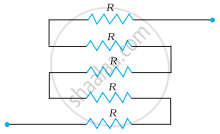
Determine the equivalent resistance of networks shown in Fig.
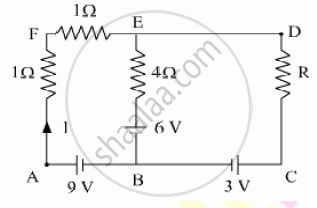
Using Kirchhoff’s rules determine the value of unknown resistance R in the circuit so that no current flows through 4 Ω resistance. Also find the potential difference between A and D.
Twelve wires, each of equal resistance r, are joined to form a cube, as shown in the figure. Find the equivalent resistance between the diagonally-opposite points a and f.

Consider the potentiometer circuit as arranged in the figure. The potentiometer wire is 600 cm long. (a) At what distance from the point A should the jockey touch the wire to get zero deflection in the galvanometer? (b) If the jockey touches the wire at a distance of 560 cm from A, what will be the current in the galvanometer?
On which conservation principle is Kirchoff's Second Law of electrical networks based?
Twelve wires each having a resistance of 3 Ω are connected to form a cubical network. A battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of this network. Determine its equivalent resistance and the current along each edge of the cube.
State and explain Kirchhoff’s rules.
Obtain the condition for bridge balance in Wheatstone’s bridge.
The Kirchhoff's second law (ΣiR = ΣE), where the symbols have their usual meanings, is based on ______.
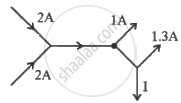
The figure below shows current in a part of electric circuit. The current I is ______.
What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate `R_(unknown)` by any other method?
What is the advantage of using thick metallic strips to join wires in a potentiometer?
Power P is to be delivered to a device via transmission cables having resistance RC. If V is the voltage across R and I the current through it, find the power wasted and how can it be reduced.
Derive the equation of the balanced state in a Wheatstone bridge using Kirchhoff’s laws.
