Advertisements
Advertisements
प्रश्न
In the given circuit, assuming point A to be at zero potential, use Kirchhoff’s rules to determine the potential at point B.
Advertisements
उत्तर
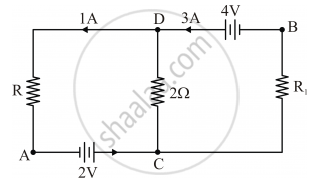
According to Kirchhoff’s Junction Law, when applied at junction D:
Incoming current = outgoing current
So, 3A = 1A + current through 2Ω.
Hence, current through 2Ω is 2A from D to C. Applying Kirchhoff’s law to the loop containing R1, 2Ω and 4V.
3A is the current through R1 as the current coming out from the 4V battery is 3A.
4 = 3 × R1 + 2 × 2
⇒ R1 = 0 Ω
So, no potential drop between B and C.
Now lets analyse the bigger loop containing 4V, R and 2V (R1 can be omitted now); here the 4V and 2V are connected in series with B as a point between the two batteries. So we finally have the potential at B to be 2V.
APPEARS IN
संबंधित प्रश्न
State Kirchhoff's rules for an electric network. Using Kirchhoff's rules, obtain the balance condition in terms of the resistances of four arms of Wheatstone bridge.
An infinite ladder is constructed with 1 Ω and 2 Ω resistors, as shown in the figure. (a) Find the effective resistance between the points A and B. (b) Find the current that passes through the 2 Ω resistor nearest to the battery.
Consider the potentiometer circuit as arranged in the figure. The potentiometer wire is 600 cm long. (a) At what distance from the point A should the jockey touch the wire to get zero deflection in the galvanometer? (b) If the jockey touches the wire at a distance of 560 cm from A, what will be the current in the galvanometer?
Solve the following question.
Using Kirchhoff’s rules, calculate the current through the 40 Ω and 20 Ω resistors in the following circuit.
Kirchhoff’s second law is a consequence of law of conservation of ______.
The Kirchhoff's second law (ΣiR = ΣE), where the symbols have their usual meanings, is based on ______.
While measuring the length of the rod by vernier callipers, the reading on the main scale is 6.4 cm and the eight divisions on vernier is in line with marking on the main scale division. If the least count of callipers is 0.01 and zero error - 0.04 cm, the length of the rod is ______.
Kirchhoff s second law is based on the law of conservation of ______
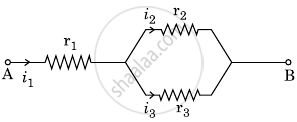
Three resistors having resistances r1, r2 and r3 are connected as shown in the given circuit. The ratio `i_3/i_1` of currents in terms of resistances used in the circuit is:
What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate `R_(unknown)` by any other method?
