Advertisements
Advertisements
Question
In the given circuit, assuming point A to be at zero potential, use Kirchhoff’s rules to determine the potential at point B.

Solution
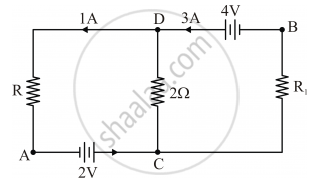
According to Kirchhoff’s Junction Law, when applied at junction D:
Incoming current = outgoing current
So, 3A = 1A + current through 2Ω.
Hence, current through 2Ω is 2A from D to C. Applying Kirchhoff’s law to the loop containing R1, 2Ω and 4V.
3A is the current through R1 as the current coming out from the 4V battery is 3A.
4 = 3 × R1 + 2 × 2
⇒ R1 = 0 Ω
So, no potential drop between B and C.
Now lets analyse the bigger loop containing 4V, R and 2V (R1 can be omitted now); here the 4V and 2V are connected in series with B as a point between the two batteries. So we finally have the potential at B to be 2V.
APPEARS IN
RELATED QUESTIONS
State the two Kirchhoff’s rules used in electric networks. How are there rules justified?
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of 6 Ω?
State Kirchhoff's rules for an electric network. Using Kirchhoff's rules, obtain the balance condition in terms of the resistances of four arms of Wheatstone bridge.
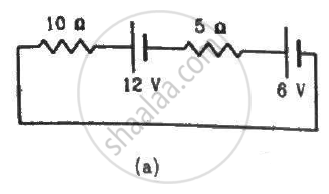
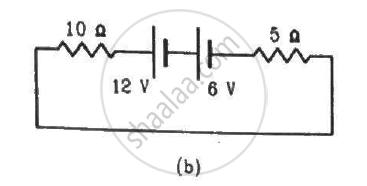
Consider the circuit shown in the figure. Find (a) the current in the circuit (b) the potential drop across the 5 Ω resistor (c) the potential drop across the 10 Ω resistor (d) Answer the parts (a), (b) and (c) with reference to the figure.
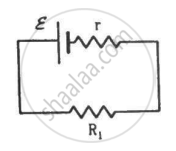
Two unequal resistances, R1 and R2, are connected across two identical batteries of emf ε and internal resistance r (see the figure). Can the thermal energies developed in R1 and R2 be equal in a given time? If yes, what will be the condition?
On which conservation principle is Kirchoff's Second Law of electrical networks based?
State Kirchhoff’s current rule.
State and explain Kirchhoff’s rules.
How the emf of two cells are compared using potentiometer?
State the two Kirchhoff’s rules used in the analysis of electric circuits and explain them.
