Advertisements
Advertisements
Question
Using the curve for the binding energy per nucleon as a function of mass number A, state clearly how the release in energy in the processes of nuclear fission and nuclear fusion can be explained.
Solution
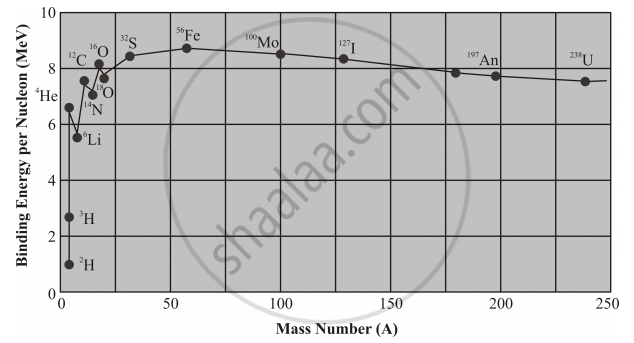
The rising of the binding energy curve at low mass numbers, indicates that energy will be released if two nuclides of small mass number combine to form a single middle-mass nuclide. This process is called nuclear fusion.
Highest peak (Fe) represents the most stable nucleus and all the other nuclei tend to achieve this state by undergoing nuclear reaction.
The eventual dropping of the binding energy curve at high mass numbers indicates that nucleons are more tightly bound when they are assembled into two middle-mass nuclides rather than into a single high-mass nuclide. Hence energy can be released by the nuclear fission, or splitting, of a single massive nucleus into two smaller fragments.
APPEARS IN
RELATED QUESTIONS
In a typical nuclear reaction, e.g.
`"_1^2H+"_1^2H ->"_2^3He + n + 3.27 \text { MeV },`
although number of nucleons is conserved, yet energy is released. How? Explain.
Draw the plot of binding energy per nucleon (BE/A) as a functino of mass number A. Write two important conclusions that can be drawn regarding the nature of nuclear force.
A heavy nucleus X of mass number 240 and binding energy per nucleon 7.6 MeV is split into two fragments Y and Z of mass numbers 110 and 130. The binding energy of nucleons in Y and Z is 8.5 MeV per nucleon. Calculate the energy Q released per fission in MeV.
As the mass number A increases, the binding energy per nucleon in a nucleus
Which of the following is a wrong description of binding energy of a nucleus?
In one average-life,
A neutron star has a density equal to that of the nuclear matter. Assuming the star to be spherical, find the radius of a neutron star whose mass is 4.0 × 1030 kg (twice the mass of the sun).
Calculate the mass of an α-particle. Its Its binding energy is 28.2 MeV.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
(a) Calculate the energy released if 238U emits an α-particle. (b) Calculate the energy to be supplied to 238U it two protons and two neutrons are to be emitted one by one. The atomic masses of 238U, 234Th and 4He are 238.0508 u, 234.04363 u and 4.00260 u respectively.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
A nucleus of mass M emits a γ-ray photon of frequency 'v'. The loss of internal energy by the nucleus is ______.
