Advertisements
Advertisements
Question
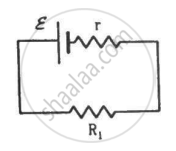
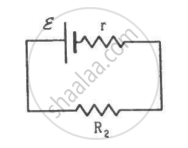
Two unequal resistances, R1 and R2, are connected across two identical batteries of emf ε and internal resistance r (see the figure). Can the thermal energies developed in R1 and R2 be equal in a given time? If yes, what will be the condition?
Solution
For the given time t, let the currents passing through the resistance R1 and R2 be i1 and i2, respectively.
Applying Kirchoff's Voltage Law to circuit-1, we get:-
\[\epsilon - i_1 r - i_1 R_1 = 0\]
\[ \Rightarrow i_1 = \frac{\epsilon}{r + R_1}\]
Similarly, the current in the other circuit,
\[i_2 = \frac{\epsilon}{r + R_2}\]
The thermal energies through the resistances are given by
\[i_1^2 R_1 t = i_2^2 R_2 t\]
\[ \left( \frac{\epsilon}{r + R_1} \right)^2 R_1 t = \left( \frac{\epsilon}{r + R_2} \right)^2 R_2 t\]
\[\frac{R_1}{\left( r + R_1 \right)^2} = \frac{R_2}{\left( r + R_2 \right)^2}\]
\[\frac{\left( r^2 + {R_1}^2 + 2r R_1 \right)}{R_1} = \frac{\left( r^2 + {R_2}^2 + 2r R_2 \right)}{R_2}\]
\[\frac{r^2}{R_1} + R_1 = \frac{r^2}{R_2} + R_2 \]
\[ r^2 \left( \frac{1}{R_1} - \frac{1}{R_2} \right) = R_2 - R_1 \]
\[ r^2 \times \frac{R_2 - R_1}{R_1 R_2} = R_2 - R_1 \]
\[ r^2 = R_1 R_2 \]
\[ \Rightarrow r = \sqrt{R_1 R_2}\]
APPEARS IN
RELATED QUESTIONS
Kirchhoff's voltage law and current law are respectively in accordance with the conservation of .................................. .
- charge and momentum
- charge and energy
- energy and charge
- energy and momentum
Kirchhoff's junction law is equivalent to .............................
(a) conservation of energy.
(b) conservation of charge
(c) conservation of electric potential
(d) conservation of electric flux
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (6/11) Ω?
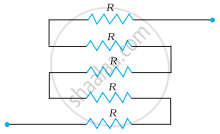
Determine the equivalent resistance of networks shown in Fig.
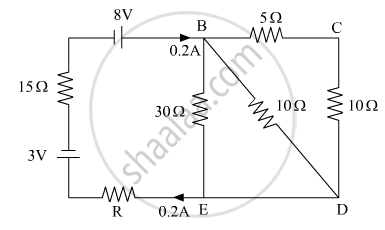
Calculate the value of the resistance R in the circuit shown in the figure so that the current in the circuit is 0.2 A. What would b the potential difference between points B and E?
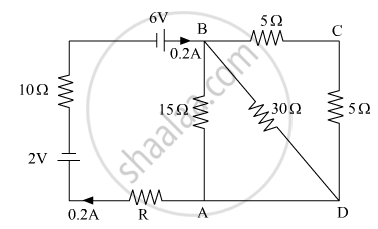
Calculate the value of the resistance R in the circuit shown in the figure so that the current in the circuit is 0.2 A. What would b the potential difference between points A and B?
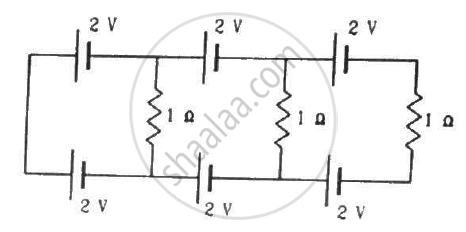
Find the circuit in the three resistors shown in the figure.
Consider the potentiometer circuit as arranged in the figure. The potentiometer wire is 600 cm long. (a) At what distance from the point A should the jockey touch the wire to get zero deflection in the galvanometer? (b) If the jockey touches the wire at a distance of 560 cm from A, what will be the current in the galvanometer?
Twelve wires each having a resistance of 3 Ω are connected to form a cubical network. A battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of this network. Determine its equivalent resistance and the current along each edge of the cube.
How the emf of two cells are compared using potentiometer?
Lightning is a very good example of a natural current. In typical lightning, there is 109 J energy transfer across the potential difference of 5 × 107 V during a time interval of 0.2 s. Using this information, estimate the following quantities:
- the total amount of charge transferred between cloud and ground
- the current in the lightning bolt
- the power delivered in 0.2 s.

A copper wire of 10-6 m2 area of cross-section, carries a current of 2 A. If the number of electrons per cubic meter is 8 × 1028, calculate the current density and average drift velocity.
A potentiometer wire has a length of 4 m and resistance of 20 Ω. It is connected in series with resistance of 2980 Ω and a cell of emf 4 V. Calculate the potential along the wire.
Three resistors having resistances r1, r2 and r3 are connected as shown in the given circuit. The ratio `i_3/i_1` of currents in terms of resistances used in the circuit is: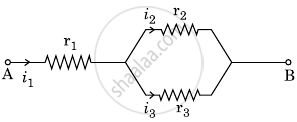
What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate `R_(unknown)` by any other method?
Two cells of voltage 10V and 2V and internal resistances 10Ω and 5Ω respectively, are connected in parallel with the positive end of 10V battery connected to negative pole of 2V battery (Figure). Find the effective voltage and effective resistance of the combination.
A 6-volt battery is connected to the terminals of a three-metre-long wire of uniform thickness and resistance of 100 ohms. The difference of potential between two points on the wire separated by a distance of 50 cm will be ______.
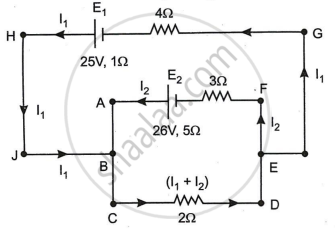
In the circuit shown in Figure below, E1 and E2 are batteries having emfs of 25V and 26V. They have an internal resistance of 1 Ω and 5 Ω respectively. Applying Kirchhoff’s laws of electrical networks, calculate the currents I1 and I2.