Advertisements
Advertisements
Question
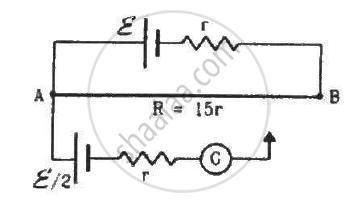
Consider the potentiometer circuit as arranged in the figure. The potentiometer wire is 600 cm long. (a) At what distance from the point A should the jockey touch the wire to get zero deflection in the galvanometer? (b) If the jockey touches the wire at a distance of 560 cm from A, what will be the current in the galvanometer?
Solution
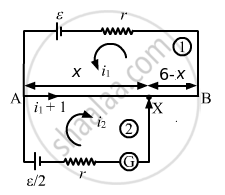
Let X be the null point on the wire at a distance x cm from point A, as shown.
Given:-
Total resistance of the wire AB = 15r
Resistance per unit cm = \[\frac{15r}{600}\]
Resistance of x cm of the wire = \[\frac{15rx}{600}\]
Resistance of (600 - x ) cm of the wire = \[\frac{15r\left( 600 - x \right)}{600}\]
(a) Applying KVL in loop 1, we get:-
\[\left( i_1 + i_2 \right)\frac{15}{600}rx + \frac{15}{600}r\left( 600 - x \right) i_1 + i_1 r = \epsilon...........(1)\]
Applying KVL in loop 2, we get:-
\[i_2 r + \frac{15}{600}rx \left( i_1 + i_2 \right) = \frac{\epsilon}{2}............(2)\]
For zero deflection in the galvanometer, i2 = 0. From equation (2),
\[\frac{15}{600}rx\left( i_1 \right) = \frac{\epsilon}{2}\]
\[ \Rightarrow i_1 = \frac{20\epsilon}{rx}\]
Substituting the values of i1 and i2 in equation (1), we get:-
x = 320 cm
(b) Putting x = 560 cm and solving equations (1) and (2), we get:-
\[i_2 = \frac{3\epsilon}{22r}\]
APPEARS IN
RELATED QUESTIONS
State the two Kirchhoff’s rules used in electric networks. How are there rules justified?
Use Kirchhoff's rules to obtain conditions for the balance condition in a Wheatstone bridge.
Determine the current in each branch of the network shown in figure.

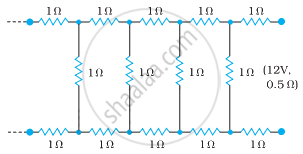
Determine the current drawn from a 12 V supply with internal resistance 0.5 Ω by the infinite network shown in the figure. Each resistor has 1 Ω resistance.
State Kirchhoff's rules and explain on what basis they are justified.
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of 6 Ω?
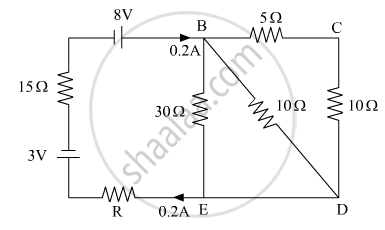
Calculate the value of the resistance R in the circuit shown in the figure so that the current in the circuit is 0.2 A. What would b the potential difference between points B and E?
Find the circuit in the three resistors shown in the figure.
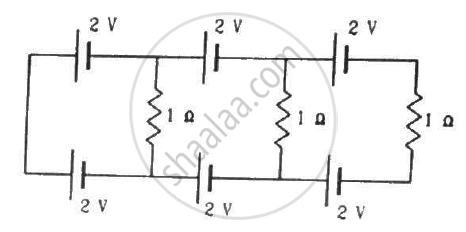
Consider the circuit shown in the figure. Find (a) the current in the circuit (b) the potential drop across the 5 Ω resistor (c) the potential drop across the 10 Ω resistor (d) Answer the parts (a), (b) and (c) with reference to the figure.
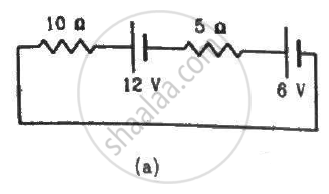
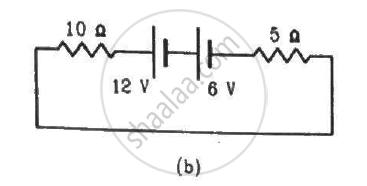
Solve the following question.
Using Kirchhoff’s rules, calculate the current through the 40 Ω and 20 Ω resistors in the following circuit.

State Kirchhoff ’s voltage rule.
State and explain Kirchhoff’s rules.
A copper wire of 10-6 m2 area of cross-section, carries a current of 2 A. If the number of electrons per cubic meter is 8 × 1028, calculate the current density and average drift velocity.
A potentiometer wire has a length of 4 m and resistance of 20 Ω. It is connected in series with resistance of 2980 Ω and a cell of emf 4 V. Calculate the potential along the wire.
Kirchhoff s second law is based on the law of conservation of ______
In a meter bridge the point D is a neutral point (Figure).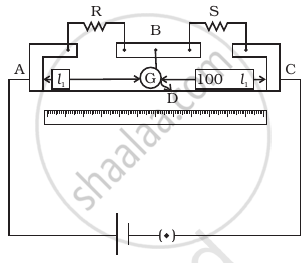
- The meter bridge can have no other neutral point for this set of resistances.
- When the jockey contacts a point on meter wire left of D, current flows to B from the wire.
- When the jockey contacts a point on the meter wire to the right of D, current flows from B to the wire through galvanometer.
- When R is increased, the neutral point shifts to left.
Two cells of voltage 10V and 2V and internal resistances 10Ω and 5Ω respectively, are connected in parallel with the positive end of 10V battery connected to negative pole of 2V battery (Figure). Find the effective voltage and effective resistance of the combination.
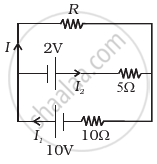
State the two Kirchhoff’s rules used in the analysis of electric circuits and explain them.
