Advertisements
Advertisements
Question
Solve the following question.
Using Kirchhoff’s rules, calculate the current through the 40 Ω and 20 Ω resistors in the following circuit.
Advertisements
Solution
Apply KVL through ABCDA
`80 - 20i_1 - 40(i_1 - i_2) = 0`
`80 - 60i_1 + 40i_2 = 0` ....(1)
Apply KVL through FEDCF
`40 + 40(i_1 - i_2) - 10i_2 = 0`
`40 + 40i_1 - 50i_2 = 0` ......(2)
`4i_2 - 6i_1 = -8 (1)` .....[ from (1)]
`-5i_2 + 4i_1 = -4 (2)` .....[ from (2)]
Multiply equation (2) by `6/4` and add with equation (1)
`4i_2 - 6i_1 = -8`
`(-30i_2)/4 + 6i_1 = -6`
__________________________
`4i_2 - 30/4i_2 = -14`
`(-14)/4i_2 = -14`
`i_2 = (-14)/7 xx 2`
`i_2 = 4 A`
Put the value of i2 in equation (1)
`4 xx (4) - 6i_1 = -8`
`16 - 6i_1 = -8`
`6i_1 = 16 + 8 = 24`
`i_1 = 4A`
So, current through 40 Ω resistor = `i_1 - i_2`
= 4 - 4
= 0 A
Hence, current through 20 Ω resistor = 4A.
RELATED QUESTIONS
The current is drawn from a cell of emf E and internal resistance r connected to the network of resistors each of resistance r as shown in the figure. Obtain the expression for
- the current draw from the cell and
- the power consumed in the network.
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (6/11) Ω?
Determine the equivalent resistance of networks shown in Fig.
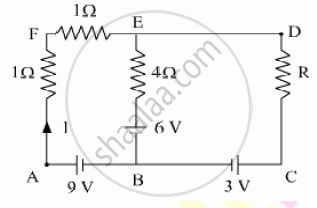
Using Kirchhoff’s rules determine the value of unknown resistance R in the circuit so that no current flows through 4 Ω resistance. Also find the potential difference between A and D.
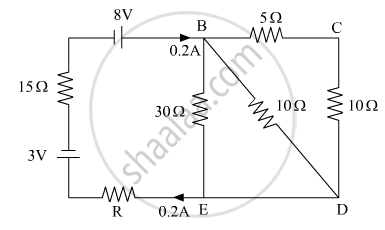
Calculate the value of the resistance R in the circuit shown in the figure so that the current in the circuit is 0.2 A. What would b the potential difference between points B and E?
Two unequal resistances, R1 and R2, are connected across two identical batteries of emf ε and internal resistance r (see the figure). Can the thermal energies developed in R1 and R2 be equal in a given time? If yes, what will be the condition?
On which conservation principle is Kirchoff's Second Law of electrical networks based?
State Kirchhoff ’s voltage rule.
State the principle of potentiometer.
State and explain Kirchhoff’s rules.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63 cm, what is the emf of the second cell?
Kirchhoff’s second law is a consequence of law of conservation of ______.
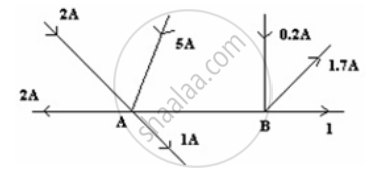
Figure shows current in a part of an electrical circuit. Then current I is ______.
Three resistors having resistances r1, r2 and r3 are connected as shown in the given circuit. The ratio `i_3/i_1` of currents in terms of resistances used in the circuit is:
In a meter bridge the point D is a neutral point (Figure).
- The meter bridge can have no other neutral point for this set of resistances.
- When the jockey contacts a point on meter wire left of D, current flows to B from the wire.
- When the jockey contacts a point on the meter wire to the right of D, current flows from B to the wire through galvanometer.
- When R is increased, the neutral point shifts to left.
What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate `R_(unknown)` by any other method?
Derive the equation of the balanced state in a Wheatstone bridge using Kirchhoff’s laws.
The figure below shows two batteries, E1 and E2, having emfs of 18V and 10V and internal resistances of 1 Ω and 2 Ω, respectively. W1, W2 and W3 are uniform metallic wires AC, FD and BE having resistances of 8 Ω, 6 Ω and 10 Ω respectively. B and E are midpoints of the wires W1 and W2. Using Kirchhoff's laws of electrical circuits, calculate the current flowing in the wire W3:
A constant voltage of 50 V is maintained between the points A and B of the circuit shown in the figure. The current through the branch CD of the circuit is:
