Advertisements
Advertisements
Question
Explain the determination of unknown resistance using meter bridge.
Solution
The meter bridge is another form of Wheatstone’s bridge. It consists of a uniform manganin wire AB of one meter length. This wire is stretched along a meter scale on a wooden board between two copper strips C and D. Between these two copper strips another copper strip E is mounted to enclose two gaps G1 and G2 An unknown resistance P is connected in G1 and a standard resistance Q is connected in G2.
A jockey (conducting wire) is connected to the terminal E on the central copper strip through a galvanometer (G) and a high resistance (HR). The exact position of jockey on the wire can be read on the scale. A Lechlanche cell and a key (K) are connected across the ends of the bridge wire.

Meter bridge
The position of the jockey on the wire is adjusted so that the galvanometer shows zero deflection. Let the point be J. The lengths AJ and JB of the bridge wire now replace the resistance R and S of the Wheatstone’s bridge. Then
`"P"/"Q" = "R"/"S" = ("R"' *"AJ")/("R"'*"JB")` ....(1)
where R’ is the resistance per unit length of wire
`"P"/"Q" = "AJ"/"JB" = l_1/l_2` ....(2)
P = Q `l_1/l_2` ....(3)
The bridge wire is soldered at the ends of the copper strips. Due to imperfect contact, some resistance might be introduced at the contact. These are called end resistances. This error can be eliminated, if another set of readings are taken with P and Q interchanged and the average value of P is found.
To find the specific resistance of the material of the wire in the coil P, the radius r and length l of the wire is measured. The specific resistance or resistivity r can be calculated using the relation.
Resistance = ρ - `l/"A"`
By rearranging the above equation, we get
ρ = Resistance `xx "A"/l`
If P is the unknown resistance, equation (4) becomes
ρ = P`(pi"r"^2)/l`
APPEARS IN
RELATED QUESTIONS
Kirchhoff's voltage law and current law are respectively in accordance with the conservation of .................................. .
- charge and momentum
- charge and energy
- energy and charge
- energy and momentum
Kirchhoff's junction law is equivalent to .............................
(a) conservation of energy.
(b) conservation of charge
(c) conservation of electric potential
(d) conservation of electric flux
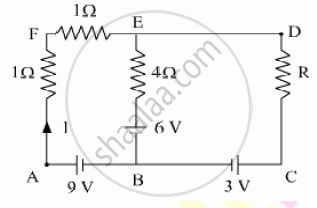
Using Kirchhoff’s rules determine the value of unknown resistance R in the circuit so that no current flows through 4 Ω resistance. Also find the potential difference between A and D.
An infinite ladder is constructed with 1 Ω and 2 Ω resistors, as shown in the figure. (a) Find the effective resistance between the points A and B. (b) Find the current that passes through the 2 Ω resistor nearest to the battery.

A capacitor of capacitance 8.0 μF is connected to a battery of emf 6.0 V through a resistance of 24 Ω. Find the current in the circuit (a) just after the connections are made and (b) one time constant after the connections are made.
On which conservation principle is Kirchoff's Second Law of electrical networks based?
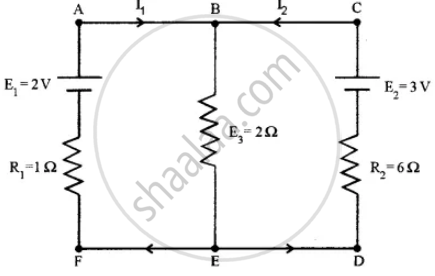
In the circuit shown in the figure below, E1 and E2 are two cells having emfs 2 V and 3 V respectively, and negligible internal resistance. Applying Kirchhoff’s laws of electrical networks, find the values of currents l1 and I2.
A potentiometer wire has a length of 4 m and resistance of 20 Ω. It is connected in series with resistance of 2980 Ω and a cell of emf 4 V. Calculate the potential along the wire.
Power P is to be delivered to a device via transmission cables having resistance RC. If V is the voltage across R and I the current through it, find the power wasted and how can it be reduced.
The circuit in figure shows two cells connected in opposition to each other. Cell E1 is of emf 6V and internal resistance 2Ω; the cell E2 is of emf 4V and internal resistance 8Ω. Find the potential difference between the points A and B.
