Advertisements
Advertisements
प्रश्न
Explain the determination of unknown resistance using meter bridge.
उत्तर
The meter bridge is another form of Wheatstone’s bridge. It consists of a uniform manganin wire AB of one meter length. This wire is stretched along a meter scale on a wooden board between two copper strips C and D. Between these two copper strips another copper strip E is mounted to enclose two gaps G1 and G2 An unknown resistance P is connected in G1 and a standard resistance Q is connected in G2.
A jockey (conducting wire) is connected to the terminal E on the central copper strip through a galvanometer (G) and a high resistance (HR). The exact position of jockey on the wire can be read on the scale. A Lechlanche cell and a key (K) are connected across the ends of the bridge wire.

Meter bridge
The position of the jockey on the wire is adjusted so that the galvanometer shows zero deflection. Let the point be J. The lengths AJ and JB of the bridge wire now replace the resistance R and S of the Wheatstone’s bridge. Then
`"P"/"Q" = "R"/"S" = ("R"' *"AJ")/("R"'*"JB")` ....(1)
where R’ is the resistance per unit length of wire
`"P"/"Q" = "AJ"/"JB" = l_1/l_2` ....(2)
P = Q `l_1/l_2` ....(3)
The bridge wire is soldered at the ends of the copper strips. Due to imperfect contact, some resistance might be introduced at the contact. These are called end resistances. This error can be eliminated, if another set of readings are taken with P and Q interchanged and the average value of P is found.
To find the specific resistance of the material of the wire in the coil P, the radius r and length l of the wire is measured. The specific resistance or resistivity r can be calculated using the relation.
Resistance = ρ - `l/"A"`
By rearranging the above equation, we get
ρ = Resistance `xx "A"/l`
If P is the unknown resistance, equation (4) becomes
ρ = P`(pi"r"^2)/l`
APPEARS IN
संबंधित प्रश्न
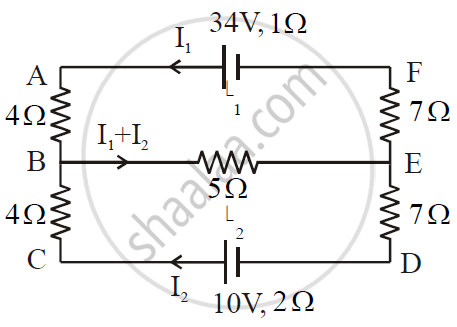
ε1 and ε2 are two batteries having emf of 34V and 10V respectively and internal resistance of 1Ω and 2Ω respectively. They are connected as shown in the figure below. Using Kirchhoff’s Laws of electrical networks, calculate the currents I1 and I2.
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (11/3) Ω?
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of 6 Ω?
Using Kirchhoff’s rules determine the value of unknown resistance R in the circuit so that no current flows through 4 Ω resistance. Also find the potential difference between A and D.
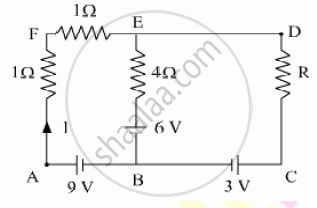
In the given circuit, assuming point A to be at zero potential, use Kirchhoff’s rules to determine the potential at point B.

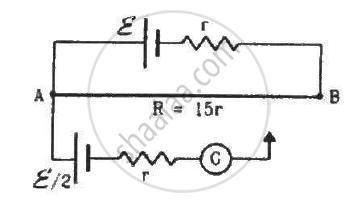
Consider the potentiometer circuit as arranged in the figure. The potentiometer wire is 600 cm long. (a) At what distance from the point A should the jockey touch the wire to get zero deflection in the galvanometer? (b) If the jockey touches the wire at a distance of 560 cm from A, what will be the current in the galvanometer?
Assertion: Kirchhoff’s junction rule follows from conservation of charge.
Reason: Kirchhoff’s loop rule follows from conservation of momentum.
In a meter bridge the point D is a neutral point (Figure).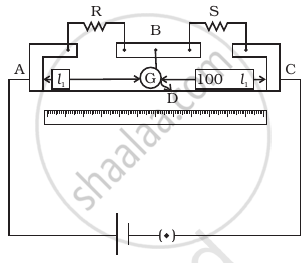
- The meter bridge can have no other neutral point for this set of resistances.
- When the jockey contacts a point on meter wire left of D, current flows to B from the wire.
- When the jockey contacts a point on the meter wire to the right of D, current flows from B to the wire through galvanometer.
- When R is increased, the neutral point shifts to left.
Derive the equation of the balanced state in a Wheatstone bridge using Kirchhoff’s laws.
A 6-volt battery is connected to the terminals of a three-metre-long wire of uniform thickness and resistance of 100 ohms. The difference of potential between two points on the wire separated by a distance of 50 cm will be ______.
