Advertisements
Advertisements
प्रश्न
Solve the following question.
Using Kirchhoff’s rules, calculate the current through the 40 Ω and 20 Ω resistors in the following circuit.

उत्तर
Apply KVL through ABCDA

`80 - 20i_1 - 40(i_1 - i_2) = 0`
`80 - 60i_1 + 40i_2 = 0` ....(1)
Apply KVL through FEDCF
`40 + 40(i_1 - i_2) - 10i_2 = 0`
`40 + 40i_1 - 50i_2 = 0` ......(2)
`4i_2 - 6i_1 = -8 (1)` .....[ from (1)]
`-5i_2 + 4i_1 = -4 (2)` .....[ from (2)]
Multiply equation (2) by `6/4` and add with equation (1)
`4i_2 - 6i_1 = -8`
`(-30i_2)/4 + 6i_1 = -6`
__________________________
`4i_2 - 30/4i_2 = -14`
`(-14)/4i_2 = -14`
`i_2 = (-14)/7 xx 2`
`i_2 = 4 A`
Put the value of i2 in equation (1)
`4 xx (4) - 6i_1 = -8`
`16 - 6i_1 = -8`
`6i_1 = 16 + 8 = 24`
`i_1 = 4A`
So, current through 40 Ω resistor = `i_1 - i_2`
= 4 - 4
= 0 A
Hence, current through 20 Ω resistor = 4A.
संबंधित प्रश्न
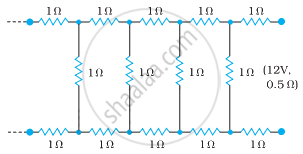
Determine the current drawn from a 12 V supply with internal resistance 0.5 Ω by the infinite network shown in the figure. Each resistor has 1 Ω resistance.
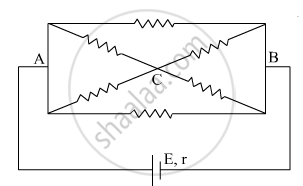
The current is drawn from a cell of emf E and internal resistance r connected to the network of resistors each of resistance r as shown in the figure. Obtain the expression for
- the current draw from the cell and
- the power consumed in the network.
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (11/5) Ω?
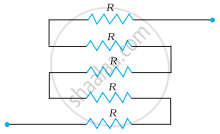
Determine the equivalent resistance of networks shown in Fig.
State Kirchhoff’s current rule.
Lightning is a very good example of a natural current. In typical lightning, there is 109 J energy transfer across the potential difference of 5 × 107 V during a time interval of 0.2 s. Using this information, estimate the following quantities:
- the total amount of charge transferred between cloud and ground
- the current in the lightning bolt
- the power delivered in 0.2 s.

The e.m.f of The battery in a thermocouple is doubled. The rate of heat generated at one of the junction will.
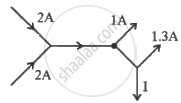
The figure below shows current in a part of electric circuit. The current I is ______.
Derive the equation of the balanced state in a Wheatstone bridge using Kirchhoff’s laws.
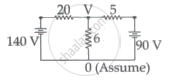
The value of current in the 6Ω resistance is ______.