Advertisements
Advertisements
प्रश्न
Answer the following question.
What is the end error in a meter bridge? How is it overcome? The resistances in the two arms of the metre bridge are R = Ω and S respectively. When the resistance S is shunted with equal resistance, the new balance length found to be 1.5 l1, where l2 is the initial balancing length. calculate the value of s.

उत्तर
The shifting of zero of the scale at different points as well as the stray resistance gives rise to the end error in meter bridge wire. This error arises due to the non-uniformity of the meter wire End corrections can be estimated by including known resistances P1 and Q1 in the two ends and finding the null point.
We have
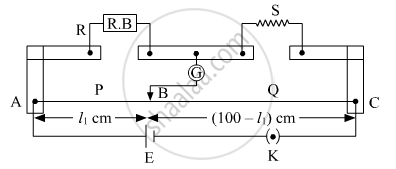
R = 5 Ω
According to wheat stone bridge principle:
`R/l_1 = S/(100 - l_1)`
`5/l_1 = S/(100 - l_1)` ....(1)
After shunting, connect the resistance in parallel
`S → S/2`
`5/(1.5 l_1) = S/(2(100 - 1.5 l_1))` ....(2)
Thus, equation (1) can be written as
`500 - 5l_1 = Sl_1` ....(3)
And equation 2 is
`10(100 - 1.5l_1) = 1.5 Sl_1` ....(4)
From equation (3) and (4)
`(500 - 5l_1)/l_1 = (1000 - 15l_1)/(1.5l_1)`
`750 - 7.5l_1 = 1000 - 15l_1`
`-250 = -7.5l_1`
`l_1 = 100/3`
S = `(500 - (5 xx 100)/3)/(100/3) = (500 - 500/3)/(100/3) = 1000/3 xx 3/100`
S = 10 Ω
संबंधित प्रश्न
The earth’s surface has a negative surface charge density of 10−9 C m−2. The potential difference of 400 kV between the top of the atmosphere and the surface results (due to the low conductivity of the lower atmosphere) in a current of only 1800 A over the entire globe. If there were no mechanism of sustaining atmospheric electric field, how much time (roughly) would be required to neutralise the earth’s surface? (This never happens in practice because there is a mechanism to replenish electric charges, namely the continual thunderstorms and lightning in different parts of the globe). (Radius of earth = 6.37 × 106 m.)
A secondary cell after long use has an emf of 1.9 V and a large internal resistance of 380 Ω. What maximum current can be drawn from the cell? Could the cell drive the starting motor of a car?
A resistor R is connected to a cell of-emf e and internal resistance r. The potential difference across the resistor R is found to be V. State the relation between e, V, Rand r.
A potentiometer wire of length 1.0 m has a resistance of 15 Ω. It is connected to a 5 V battery in series with a resistance of 5 Ω. Determine the emf of the primary cell which gives a balance point at 60 cm.
A cell of emf ‘E’ and internal resistance ‘r’ is connected across a variable resistor ‘R’. Plot a graph showing the variation of terminal potential ‘V’ with resistance R. Predict from the graph the condition under which ‘V’ becomes equal to ‘E’.
Consider N = n1n2 identical cells, each of emf ε and internal resistance r. Suppose n1 cells are joined in series to form a line and n2 such lines are connected in parallel.
The combination drives a current in an external resistance R. (a) Find the current in the external resistance. (b) Assuming that n1 and n2 can be continuously varied, find the relation between n1, n2, R and r for which the current in R is maximum.
Answer the following question.
A cell of emf E and internal resistance r is connected across a variable resistor R. Plot the shape of graphs showing a variation of terminal voltage V with (i) R and (ii) circuit current I.
If n cells each of emf e and internal resistance r are connected in parallel, then the total emf and internal resistance will be ______.
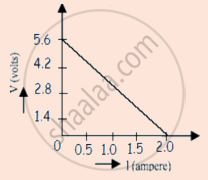
A straight line plot showing the terminal potential difference (V) of a cell as a function of current (I) drawn from it, is shown in the figure. The internal resistance of the cell would be then ______.
Three cells, each of emf E but internal resistances 2r, 3r and 6r are connected in parallel across a resistor R.
Obtain expressions for (i) current flowing in the circuit, and (ii) the terminal potential differences across the equivalent cell.
