Advertisements
Advertisements
प्रश्न
Answer the following question.
What is the end error in a meter bridge? How is it overcome? The resistances in the two arms of the metre bridge are R = Ω and S respectively. When the resistance S is shunted with equal resistance, the new balance length found to be 1.5 l1, where l2 is the initial balancing length. calculate the value of s.

उत्तर
The shifting of zero of the scale at different points as well as the stray resistance gives rise to the end error in meter bridge wire. This error arises due to the non-uniformity of the meter wire End corrections can be estimated by including known resistances P1 and Q1 in the two ends and finding the null point.
We have
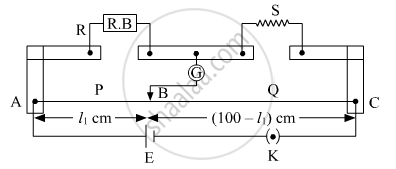
R = 5 Ω
According to wheat stone bridge principle:
`R/l_1 = S/(100 - l_1)`
`5/l_1 = S/(100 - l_1)` ....(1)
After shunting, connect the resistance in parallel
`S → S/2`
`5/(1.5 l_1) = S/(2(100 - 1.5 l_1))` ....(2)
Thus, equation (1) can be written as
`500 - 5l_1 = Sl_1` ....(3)
And equation 2 is
`10(100 - 1.5l_1) = 1.5 Sl_1` ....(4)
From equation (3) and (4)
`(500 - 5l_1)/l_1 = (1000 - 15l_1)/(1.5l_1)`
`750 - 7.5l_1 = 1000 - 15l_1`
`-250 = -7.5l_1`
`l_1 = 100/3`
S = `(500 - (5 xx 100)/3)/(100/3) = (500 - 500/3)/(100/3) = 1000/3 xx 3/100`
S = 10 Ω
संबंधित प्रश्न
Two identical cells of emf 1.5 V each joined in parallel, supply energy to an external circuit consisting of two resistances of 7 Ω each joined in parallel. A very high resistance voltmeter reads the terminal voltage of cells to be 1.4 V. Calculate the internal resistance of each cell.
A long straight current carrying wire passes normally through the centre of circular loop. If the current through the wire increases, will there be an induced emf in the loop? Justify.
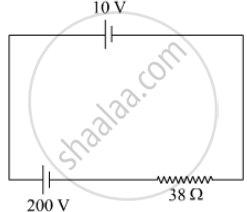
A 10 V cell of negligible internal resistance is connected in parallel across a battery of emf 200 V and internal resistance 38 Ω as shown in the figure. Find the value of current in the circuit.
Two non-ideal batteries are connected in parallel. Consider the following statements:-
(A) The equivalent emf is smaller than either of the two emfs.
(B) The equivalent internal resistance is smaller than either of the two internal resistances.
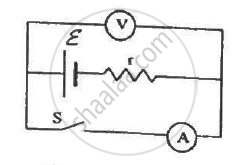
The following figure shows an arrangement to measure the emf ε and internal resistance r of a battery. The voltmeter has a very high resistance and the ammeter also has some resistance. The voltmeter reads 1.52 V when the switch S is open. When the switch is closed, the voltmeter reading drops to 1.45 V and the ammeter reads 1.0 A. Find the emf and the internal resistance of the battery.
Consider N = n1n2 identical cells, each of emf ε and internal resistance r. Suppose n1 cells are joined in series to form a line and n2 such lines are connected in parallel.
The combination drives a current in an external resistance R. (a) Find the current in the external resistance. (b) Assuming that n1 and n2 can be continuously varied, find the relation between n1, n2, R and r for which the current in R is maximum.
A battery of emf 100 V and a resistor of resistance 10 kΩ are joined in series. This system is used as a source to supply current to an external resistance R. If R is not greater than 100 Ω, the current through it is constant up to two significant digits.
Find its value. This is the basic principle of a constant-current source.
A plate of area 10 cm2 is to be electroplated with copper (density 9000 kg m−3) to a thickness of 10 micrometres on both sides, using a cell of 12 V. Calculate the energy spent by the cell in the process of deposition. If this energy is used to heat 100 g of water, calculate the rise in the temperature of the water. ECE of copper = 3 × 10−7 kg C−1and specific heat capacity of water = 4200 J kg−1.
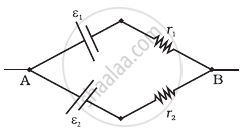
Two batteries of emf ε1 and ε2 (ε2 > ε1) and internal resistances r1 and r2 respectively are connected in parallel as shown in figure.
Three cells, each of emf E but internal resistances 2r, 3r and 6r are connected in parallel across a resistor R.
Obtain expressions for (i) current flowing in the circuit, and (ii) the terminal potential differences across the equivalent cell.
