Advertisements
Advertisements
प्रश्न
Solve the following question.
Using Kirchhoff’s rules, calculate the current through the 40 Ω and 20 Ω resistors in the following circuit.

उत्तर
Apply KVL through ABCDA

`80 - 20i_1 - 40(i_1 - i_2) = 0`
`80 - 60i_1 + 40i_2 = 0` ....(1)
Apply KVL through FEDCF
`40 + 40(i_1 - i_2) - 10i_2 = 0`
`40 + 40i_1 - 50i_2 = 0` ......(2)
`4i_2 - 6i_1 = -8 (1)` .....[ from (1)]
`-5i_2 + 4i_1 = -4 (2)` .....[ from (2)]
Multiply equation (2) by `6/4` and add with equation (1)
`4i_2 - 6i_1 = -8`
`(-30i_2)/4 + 6i_1 = -6`
__________________________
`4i_2 - 30/4i_2 = -14`
`(-14)/4i_2 = -14`
`i_2 = (-14)/7 xx 2`
`i_2 = 4 A`
Put the value of i2 in equation (1)
`4 xx (4) - 6i_1 = -8`
`16 - 6i_1 = -8`
`6i_1 = 16 + 8 = 24`
`i_1 = 4A`
So, current through 40 Ω resistor = `i_1 - i_2`
= 4 - 4
= 0 A
Hence, current through 20 Ω resistor = 4A.
संबंधित प्रश्न
State the two Kirchhoff’s rules used in electric networks. How are there rules justified?
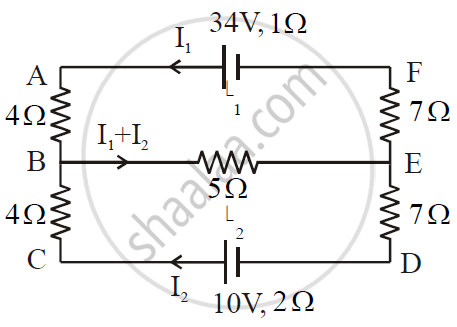
ε1 and ε2 are two batteries having emf of 34V and 10V respectively and internal resistance of 1Ω and 2Ω respectively. They are connected as shown in the figure below. Using Kirchhoff’s Laws of electrical networks, calculate the currents I1 and I2.
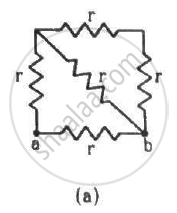
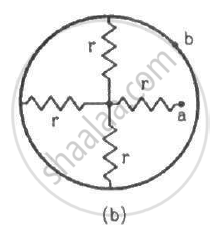
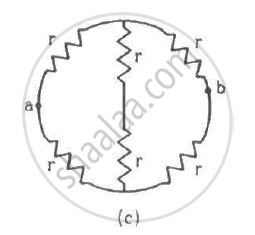
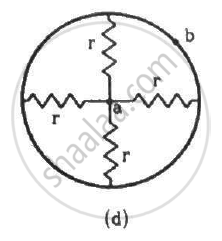
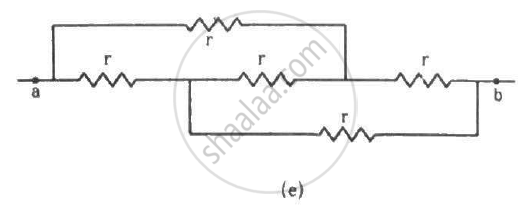
Find the equivalent resistances of the networks shown in the figure between the points a and b.
An infinite ladder is constructed with 1 Ω and 2 Ω resistors, as shown in the figure. (a) Find the effective resistance between the points A and B. (b) Find the current that passes through the 2 Ω resistor nearest to the battery.

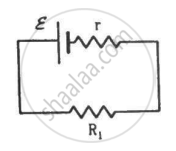
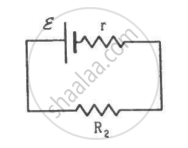
Two unequal resistances, R1 and R2, are connected across two identical batteries of emf ε and internal resistance r (see the figure). Can the thermal energies developed in R1 and R2 be equal in a given time? If yes, what will be the condition?
State Kirchhoff’s current rule.
Assertion: Kirchhoff’s junction rule follows from conservation of charge.
Reason: Kirchhoff’s loop rule follows from conservation of momentum.
What is the advantage of using thick metallic strips to join wires in a potentiometer?
State the two Kirchhoff’s rules used in the analysis of electric circuits and explain them.
A 6-volt battery is connected to the terminals of a three-metre-long wire of uniform thickness and resistance of 100 ohms. The difference of potential between two points on the wire separated by a distance of 50 cm will be ______.
