Advertisements
Advertisements
Question
In a meter bridge the point D is a neutral point (Figure).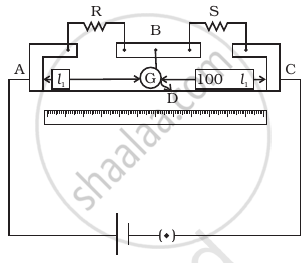
- The meter bridge can have no other neutral point for this set of resistances.
- When the jockey contacts a point on meter wire left of D, current flows to B from the wire.
- When the jockey contacts a point on the meter wire to the right of D, current flows from B to the wire through galvanometer.
- When R is increased, the neutral point shifts to left.
Options
a and c
a and d
b and c
c and d
Solution
a and c
Explanation:
In case of meter bridge, the resistance wire AC is 100 cm long. Varying the position of tapping point B, bridge is balanced. If in balanced position of bridge AB = l, BC = (100 – 1) so that Q/P = (100 – 1)/1. Also P/Q = R/S ⇒ S =(100 – 1)/1R
When there is no deflection in galvanometer there is no current across the galvanometer, then points B and D are at the same potential. That point at which the galvanometer shows no deflection is called the null point and then potential at B and neutral point D is the same. When the jockey contacts a point on the meter wire to the right of D, the potential drop across AD is more than the potential drop across AB, which brings the potential of point D less than that of B, hence current flows from B to D in the galvanometer wire.
APPEARS IN
RELATED QUESTIONS
State the two Kirchhoff’s rules used in electric networks. How are there rules justified?
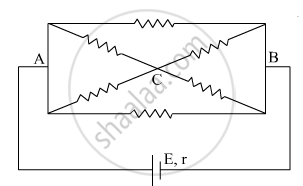
The current is drawn from a cell of emf E and internal resistance r connected to the network of resistors each of resistance r as shown in the figure. Obtain the expression for
- the current draw from the cell and
- the power consumed in the network.
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (11/3) Ω?
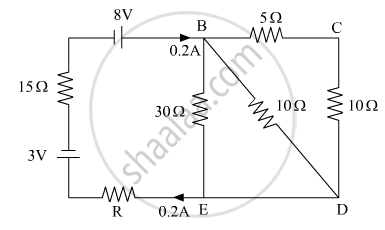
Calculate the value of the resistance R in the circuit shown in the figure so that the current in the circuit is 0.2 A. What would b the potential difference between points B and E?
Twelve wires, each of equal resistance r, are joined to form a cube, as shown in the figure. Find the equivalent resistance between the diagonally-opposite points a and f.

An infinite ladder is constructed with 1 Ω and 2 Ω resistors, as shown in the figure. (a) Find the effective resistance between the points A and B. (b) Find the current that passes through the 2 Ω resistor nearest to the battery.

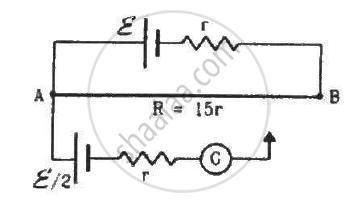
Consider the potentiometer circuit as arranged in the figure. The potentiometer wire is 600 cm long. (a) At what distance from the point A should the jockey touch the wire to get zero deflection in the galvanometer? (b) If the jockey touches the wire at a distance of 560 cm from A, what will be the current in the galvanometer?
A capacitor of capacitance 8.0 μF is connected to a battery of emf 6.0 V through a resistance of 24 Ω. Find the current in the circuit (a) just after the connections are made and (b) one time constant after the connections are made.
The e.m.f of The battery in a thermocouple is doubled. The rate of heat generated at one of the junction will.
What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate `R_(unknown)` by any other method?
