Advertisements
Advertisements
Question
Twelve wires each having a resistance of 3 Ω are connected to form a cubical network. A battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of this network. Determine its equivalent resistance and the current along each edge of the cube.
Solution
A battery of 10 V is connected across the diagonally opposite points a and f of the given network. Each side of the cube represents a 3-ohm resistor. Current entrees through the point a and leaves through the point f. Let I current is drawn from the battery and enters through point a, due to the symmetry of cube between point a and f, the current will divide itself into equal parts at each corner of the cube.
As you can see in the figure given below:
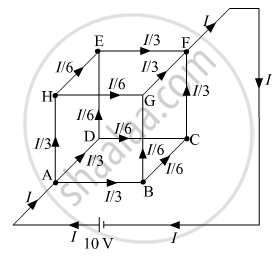
If we consider the current path ABGFA, then we can write, VA-B + VB-G + VG-F = V
⇒ `("I"/3 xx"R") + ("I"/6 xx "R") + ("I"/3 xx "R") = ("I" xx "R"_"net")`
⇒ `"R"_"net" = "R"/3 + "R"/6 + "R"/3 = (5"R")/6`
∵ R = 3Ω
⇒ `"R"_"net" = (5xx3)/6 = 2.5 Ω`
Current, `"i" = "V"/"R"_"net" = 10/2.5 = 4 "A"`
⇒ i = 4 A
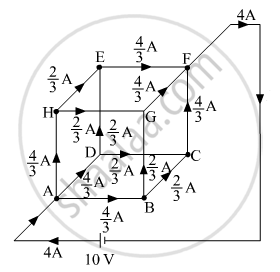
As i = 4 A, hence current through each side of the cube can be marked. The below figure shows the current through each resistance of the network. i.e. each side of the cube.
APPEARS IN
RELATED QUESTIONS
State Kirchhoff's rules and explain on what basis they are justified.
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of 6 Ω?
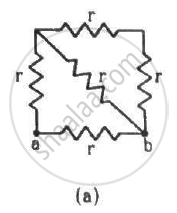
Determine the equivalent resistance of networks shown in Fig.
In the given circuit, assuming point A to be at zero potential, use Kirchhoff’s rules to determine the potential at point B.

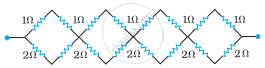
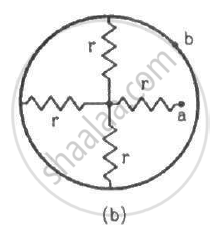
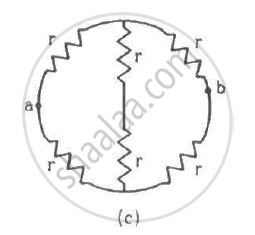
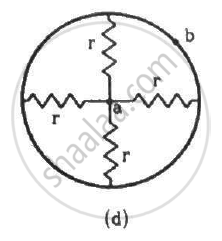
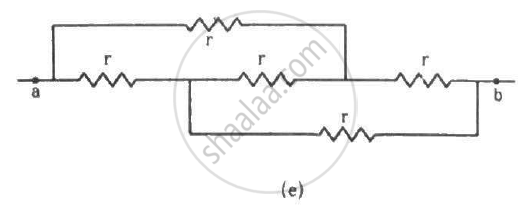
Find the equivalent resistances of the networks shown in the figure between the points a and b.
A capacitor of capacitance 8.0 μF is connected to a battery of emf 6.0 V through a resistance of 24 Ω. Find the current in the circuit (a) just after the connections are made and (b) one time constant after the connections are made.
The Kirchhoff's second law (ΣiR = ΣE), where the symbols have their usual meanings, is based on ______.
Kirchhoff s second law is based on the law of conservation of ______
What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate `R_(unknown)` by any other method?
