Advertisements
Advertisements
प्रश्न
A copper wire of 10-6 m2 area of cross-section, carries a current of 2 A. If the number of electrons per cubic meter is 8 × 1028, calculate the current density and average drift velocity.
उत्तर
A = 10-6 m2, I = 2A, n = 8 × 1028
Formula:
Current density, J = J = `"I"/"A"`
Drift velocity, `"V"_"d" = "J"/"ne"`
J = `"I"/"A" = 2/10^-6 = 2 xx 10^6`
J = `2xx10^6 "Am"^-2`
`"V"_"d" = "J"/"ne" = (2 xx 10^6)/(8 xx 10^28 xx 1.6 xx 10^-6)`
`"V"_"d" = = 0.1562 xx 10^-3`
`"V"_"d" = 15.6 xx 10^-5 "ms"^-1`
APPEARS IN
संबंधित प्रश्न
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (11/5) Ω?
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of 6 Ω?
State Kirchhoff's rules for an electric network. Using Kirchhoff's rules, obtain the balance condition in terms of the resistances of four arms of Wheatstone bridge.
Consider the potentiometer circuit as arranged in the figure. The potentiometer wire is 600 cm long. (a) At what distance from the point A should the jockey touch the wire to get zero deflection in the galvanometer? (b) If the jockey touches the wire at a distance of 560 cm from A, what will be the current in the galvanometer?
A potentiometer wire has a length of 4 m and resistance of 20 Ω. It is connected in series with resistance of 2980 Ω and a cell of emf 4 V. Calculate the potential along the wire.
The Kirchhoff's second law (ΣiR = ΣE), where the symbols have their usual meanings, is based on ______.
Two cell of 1.25 V and 0.75 V are connected parallel. The effective voltage will be:-
Power P is to be delivered to a device via transmission cables having resistance RC. If V is the voltage across R and I the current through it, find the power wasted and how can it be reduced.
Derive the equation of the balanced state in a Wheatstone bridge using Kirchhoff’s laws.
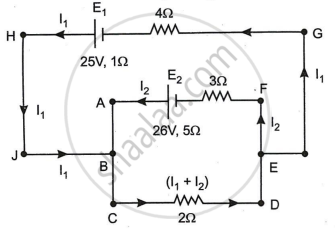
In the circuit shown in Figure below, E1 and E2 are batteries having emfs of 25V and 26V. They have an internal resistance of 1 Ω and 5 Ω respectively. Applying Kirchhoff’s laws of electrical networks, calculate the currents I1 and I2.