Advertisements
Advertisements
प्रश्न
A copper wire of 10-6 m2 area of cross-section, carries a current of 2 A. If the number of electrons per cubic meter is 8 × 1028, calculate the current density and average drift velocity.
उत्तर
A = 10-6 m2, I = 2A, n = 8 × 1028
Formula:
Current density, J = J = `"I"/"A"`
Drift velocity, `"V"_"d" = "J"/"ne"`
J = `"I"/"A" = 2/10^-6 = 2 xx 10^6`
J = `2xx10^6 "Am"^-2`
`"V"_"d" = "J"/"ne" = (2 xx 10^6)/(8 xx 10^28 xx 1.6 xx 10^-6)`
`"V"_"d" = = 0.1562 xx 10^-3`
`"V"_"d" = 15.6 xx 10^-5 "ms"^-1`
APPEARS IN
संबंधित प्रश्न
State Kirchhoff's rules and explain on what basis they are justified.
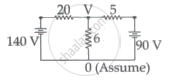
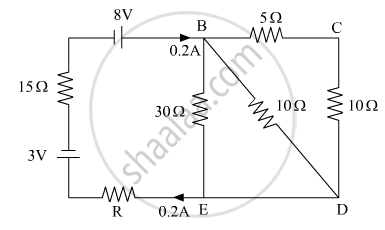
Calculate the value of the resistance R in the circuit shown in the figure so that the current in the circuit is 0.2 A. What would b the potential difference between points B and E?
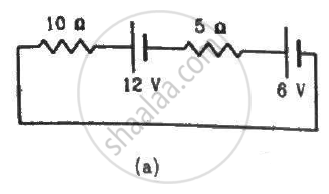
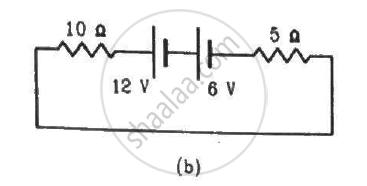
Consider the circuit shown in the figure. Find (a) the current in the circuit (b) the potential drop across the 5 Ω resistor (c) the potential drop across the 10 Ω resistor (d) Answer the parts (a), (b) and (c) with reference to the figure.
Twelve wires, each of equal resistance r, are joined to form a cube, as shown in the figure. Find the equivalent resistance between the diagonally-opposite points a and f.

Obtain the condition for bridge balance in Wheatstone’s bridge.
Explain the determination of unknown resistance using meter bridge.
Figure shows current in a part of an electrical circuit. Then current I is ______.
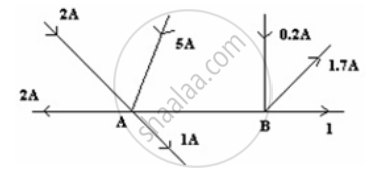
Kirchhoff’s junction rule is a reflection of ______.
- conservation of current density vector.
- conservation of charge.
- the fact that the momentum with which a charged particle approaches a junction is unchanged (as a vector) as the charged particle leaves the junction.
- the fact that there is no accumulation of charges at a junction.
The value of current in the 6Ω resistance is ______.