Advertisements
Advertisements
प्रश्न
Obtain the condition for bridge balance in Wheatstone’s bridge.
Obtain the balancing conditions in the case of Wheatstone’s bridge.
उत्तर
An important application of Kirchhoff’s rules is the Wheatstone’s Bridge. It is used to compare resistances and also helps in determining the unknown resistance in an electrical network. The bridge consists of four resistances P, Q, R, and S connected. A galvanometer G is connected between the points B and D. The battery is connected between points A and C. The current through the galvanometer is IG and its resistance is G.

Wheatstone’s bridge
Applying KirchhofFs current rule to junction B,
I1 – IG – I3 = 0 ….. (1)
Applying Kirchhoff’s current rule to junction D,
I2 + IG – I4 = 0 ….. (2)
Applying Kirchhoff’s voltage rule to loop ABDA,
I1P + IGG – I2R = 0 ….. (3)
Applying Kirchhoff’s voltage rule to loop ABCDA,
I1P + I3Q – I4S – I2R = 0 ….. (4)
When the points B and D are at the same potential, the bridge is said to be balanced. As there is no potential difference between B and D, no current flows through the galvanometer (IG = 0).
Substituting IG = 0 in equation, (1), (2) and (3), we get
I1 = I3 ….. (5)
I2 = I4 ….. (6)
I1P = I2R ….. (7)
Substituting the equation (5) and (6) in equation (4)
I1P + I1Q – I2R = 0
I1(P + Q) = I2 (R + S) ….. (8)
Dividing equation (8) by equation (7), we get
`("P + Q")/"P" = ("R + S")/"R"`
`11 + "Q"/"P" = 1 + "S"/"R"`
`=> "Q"/"P" = "S"/"R"`
`"P"/"Q" = "R"/"S"` .....(9)
This is the bridge balance condition. Only under this condition, galvanometer show null deflection. Suppose we know the values of two adjacent resistances; the other two resistances can be compared. If three of the resistances are known, the value of the unknown resistance (the fourth one) can be determined.
संबंधित प्रश्न
Kirchhoff's voltage law and current law are respectively in accordance with the conservation of .................................. .
- charge and momentum
- charge and energy
- energy and charge
- energy and momentum
State the two Kirchhoff’s rules used in electric networks. How are there rules justified?
Use Kirchhoff's rules to obtain conditions for the balance condition in a Wheatstone bridge.
Given n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?
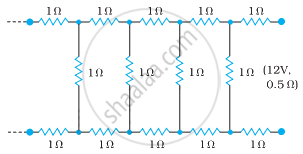
Determine the current drawn from a 12 V supply with internal resistance 0.5 Ω by the infinite network shown in the figure. Each resistor has 1 Ω resistance.
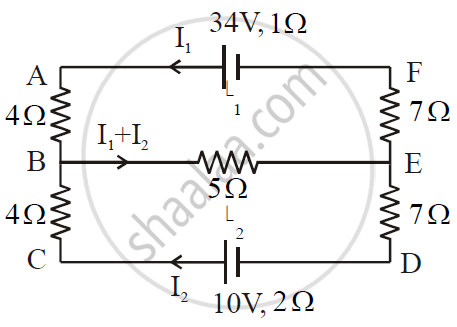
ε1 and ε2 are two batteries having emf of 34V and 10V respectively and internal resistance of 1Ω and 2Ω respectively. They are connected as shown in the figure below. Using Kirchhoff’s Laws of electrical networks, calculate the currents I1 and I2.
State Kirchhoff's rules and explain on what basis they are justified.
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (11/3) Ω?
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of 6 Ω?
State Kirchhoff's rules for an electric network. Using Kirchhoff's rules, obtain the balance condition in terms of the resistances of four arms of Wheatstone bridge.
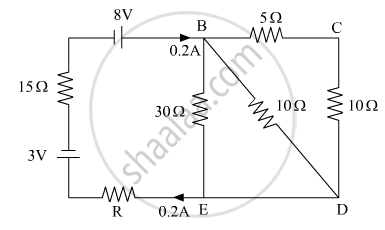
Calculate the value of the resistance R in the circuit shown in the figure so that the current in the circuit is 0.2 A. What would b the potential difference between points B and E?
Find the circuit in the three resistors shown in the figure.
Twelve wires, each of equal resistance r, are joined to form a cube, as shown in the figure. Find the equivalent resistance between the diagonally-opposite points a and f.

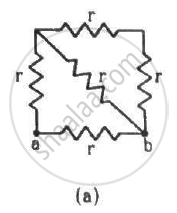
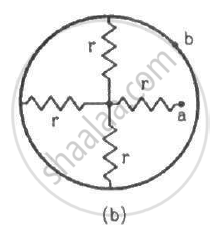
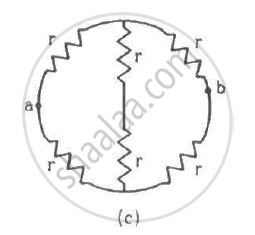
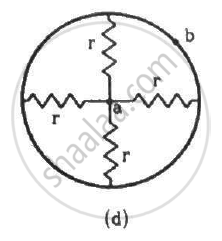
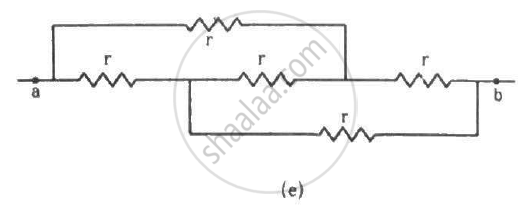
Find the equivalent resistances of the networks shown in the figure between the points a and b.
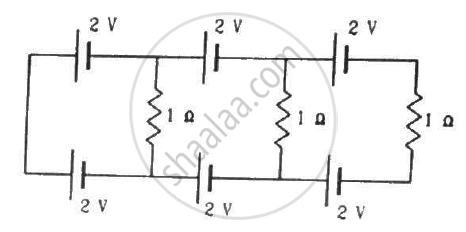
Solve the following question.
Using Kirchhoff’s rules, calculate the current through the 40 Ω and 20 Ω resistors in the following circuit.

Twelve wires each having a resistance of 3 Ω are connected to form a cubical network. A battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of this network. Determine its equivalent resistance and the current along each edge of the cube.
State Kirchhoff’s current rule.
State Kirchhoff ’s voltage rule.
State the principle of potentiometer.
Explain the determination of unknown resistance using meter bridge.
How the emf of two cells are compared using potentiometer?
A copper wire of 10-6 m2 area of cross-section, carries a current of 2 A. If the number of electrons per cubic meter is 8 × 1028, calculate the current density and average drift velocity.
Kirchhoff’s second law is a consequence of law of conservation of ______.
Assertion: Kirchhoff’s junction rule follows from conservation of charge.
Reason: Kirchhoff’s loop rule follows from conservation of momentum.
While measuring the length of the rod by vernier callipers, the reading on the main scale is 6.4 cm and the eight divisions on vernier is in line with marking on the main scale division. If the least count of callipers is 0.01 and zero error - 0.04 cm, the length of the rod is ______.
Two cell of 1.25 V and 0.75 V are connected parallel. The effective voltage will be:-
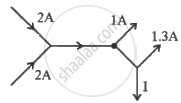
The figure below shows current in a part of electric circuit. The current I is ______.
Kirchhoff s second law is based on the law of conservation of ______
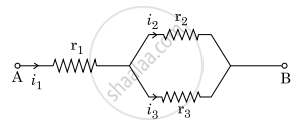
Three resistors having resistances r1, r2 and r3 are connected as shown in the given circuit. The ratio `i_3/i_1` of currents in terms of resistances used in the circuit is: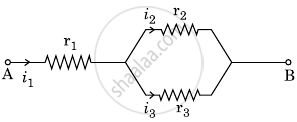
Three resistors having resistances r1, r2 and r3 are connected as shown in the given circuit. The ratio `"i"_3/"i"_1` of currents in terms of resistances used in the circuit is :
What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate `R_(unknown)` by any other method?
What is the advantage of using thick metallic strips to join wires in a potentiometer?
The circuit in figure shows two cells connected in opposition to each other. Cell E1 is of emf 6V and internal resistance 2Ω; the cell E2 is of emf 4V and internal resistance 8Ω. Find the potential difference between the points A and B.
State the two Kirchhoff’s rules used in the analysis of electric circuits and explain them.
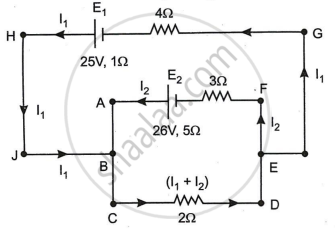
In the circuit shown in Figure below, E1 and E2 are batteries having emfs of 25V and 26V. They have an internal resistance of 1 Ω and 5 Ω respectively. Applying Kirchhoff’s laws of electrical networks, calculate the currents I1 and I2.