Advertisements
Advertisements
प्रश्न
State and explain Kirchhoff’s rules.
उत्तर
Kirchhoff’s first rule (current rule or junction rule):
Statement: It states that the algebraic sum of the currents at any junction of a circuit is zero. It is a statement of conservation of electric charge.
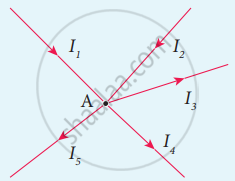
Kirchhoff ’s current rule
Explanation:
All charges that enter a given junction in a circuit must leave that junction since charge cannot build up or disappear at a junction. Current entering the junction is taken as positive and current leaving the junction is taken as negative.
Applying this law to the junction A,
I1 + I2 – I3 – I4 – I5 = o
Or
I1 + I2 = + I3 I4 + I5
Kirchhoff’s second rule (voltage rule or loop rule):
Statement: It states that in a closed circuit the algebraic sum of the products of the current and resistance of each part of the circuit is equal to the total emf included in the circuit. This rule follows from the law of conservation of energy for an isolated system. (The energy supplied by the emf sources is equal to the sum of the energy delivered to all resistors).
Explanation:
The product of current and resistance is taken as positive when the direction of the current is followed. Suppose if the direction of current is opposite to the direction of the loop, then product of current and voltage across the resistor is negative. It is shown in following Fig. (a) and (b). The emf is considered positive when proceeding from the negative to the positive terminal of the cell. It is shown in following fig. (c) and (d).
(a)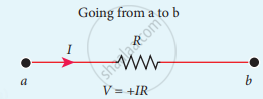
(b)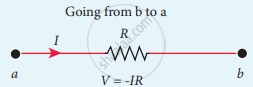
(c)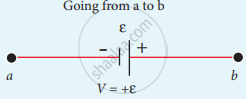
(d)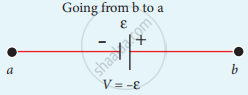
Kirchhoff voltage rule
APPEARS IN
संबंधित प्रश्न
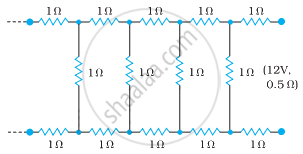
Determine the current drawn from a 12 V supply with internal resistance 0.5 Ω by the infinite network shown in the figure. Each resistor has 1 Ω resistance.
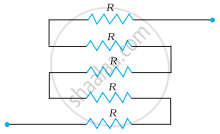
Determine the equivalent resistance of networks shown in Fig.
Determine the equivalent resistance of networks shown in Fig.
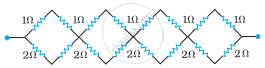
An infinite ladder is constructed with 1 Ω and 2 Ω resistors, as shown in the figure. (a) Find the effective resistance between the points A and B. (b) Find the current that passes through the 2 Ω resistor nearest to the battery.

Consider the potentiometer circuit as arranged in the figure. The potentiometer wire is 600 cm long. (a) At what distance from the point A should the jockey touch the wire to get zero deflection in the galvanometer? (b) If the jockey touches the wire at a distance of 560 cm from A, what will be the current in the galvanometer?
Twelve wires each having a resistance of 3 Ω are connected to form a cubical network. A battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of this network. Determine its equivalent resistance and the current along each edge of the cube.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63 cm, what is the emf of the second cell?
Two cell of 1.25 V and 0.75 V are connected parallel. The effective voltage will be:-
Two cells of voltage 10V and 2V and internal resistances 10Ω and 5Ω respectively, are connected in parallel with the positive end of 10V battery connected to negative pole of 2V battery (Figure). Find the effective voltage and effective resistance of the combination.
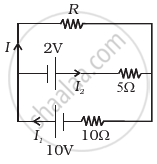
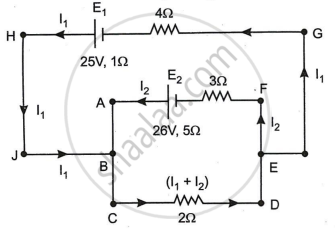
In the circuit shown in Figure below, E1 and E2 are batteries having emfs of 25V and 26V. They have an internal resistance of 1 Ω and 5 Ω respectively. Applying Kirchhoff’s laws of electrical networks, calculate the currents I1 and I2.