Advertisements
Advertisements
प्रश्न
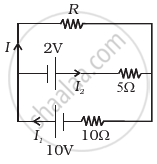
Two cells of voltage 10V and 2V and internal resistances 10Ω and 5Ω respectively, are connected in parallel with the positive end of 10V battery connected to negative pole of 2V battery (Figure). Find the effective voltage and effective resistance of the combination.
उत्तर
In this problem first, we are applying Kirchhoff's junction rule at c, I1 = I + I2
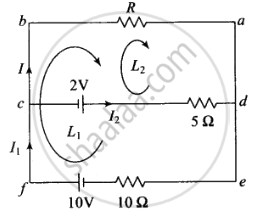
Applying Kirchhoff's voltage law in loop (e – f – b – a – e) loop L1 outer loop, then we get
10 – IR – 10l1 = 0
10 = IR + 10l1 ......(i)
Applying Kirchhoff's voltage law in loop (c – b – a – d – c) loop L2, we get
– 2 – IR + 5I2 = 0
2 = 5I2 – RI
As we know, I1 = I + I2 then
I2 = I1 – I
So the above equation can be written as
2 = 5(I1 – I) – RI
or 4 = 10I1 – 10I – 2RI ......(ii)
Subtracting equations (ii) from (i), we get
⇒ 6 = 3RI + 10I
2 = `I(R + 10/3)`
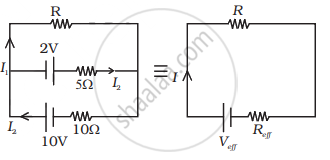
Also, the external resistance is R. The Ohm's law states that V = I(R + Reff)
On comparing, we have V = 2V and effective internal resistance `(R_("eff")) = (10/3)Ω`
Since, the equivalent internal resistance (Reff) of two cells is `(10/3)Ω`, being the parallel combination of 5Ω and 10Ω. The equivalent circuit is given below:
APPEARS IN
संबंधित प्रश्न
Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (11/3) Ω?
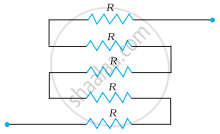
Determine the equivalent resistance of networks shown in Fig.
Using Kirchhoff’s rules determine the value of unknown resistance R in the circuit so that no current flows through 4 Ω resistance. Also find the potential difference between A and D.
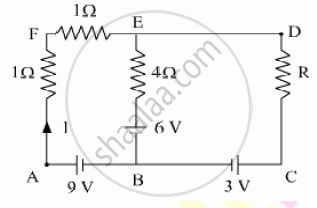
In the given circuit, assuming point A to be at zero potential, use Kirchhoff’s rules to determine the potential at point B.

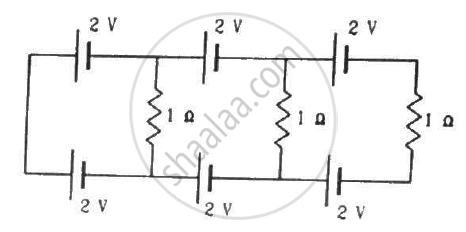
Find the circuit in the three resistors shown in the figure.
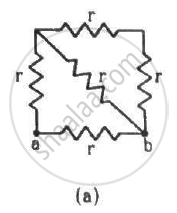
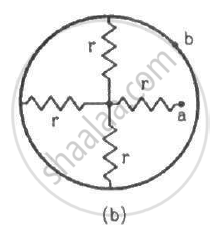
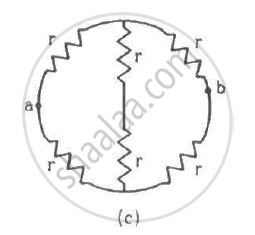
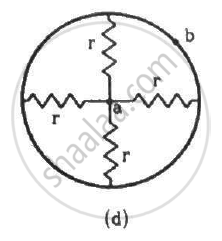
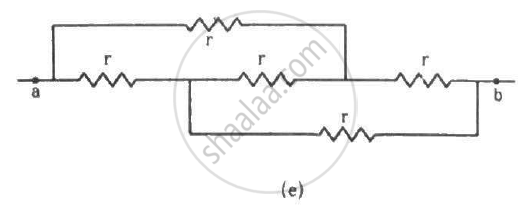
Find the equivalent resistances of the networks shown in the figure between the points a and b.
An infinite ladder is constructed with 1 Ω and 2 Ω resistors, as shown in the figure. (a) Find the effective resistance between the points A and B. (b) Find the current that passes through the 2 Ω resistor nearest to the battery.

The e.m.f of The battery in a thermocouple is doubled. The rate of heat generated at one of the junction will.
What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate `R_(unknown)` by any other method?
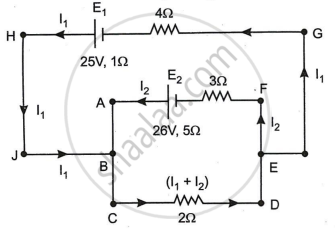
In the circuit shown in Figure below, E1 and E2 are batteries having emfs of 25V and 26V. They have an internal resistance of 1 Ω and 5 Ω respectively. Applying Kirchhoff’s laws of electrical networks, calculate the currents I1 and I2.