Advertisements
Advertisements
प्रश्न
Kirchhoff’s junction rule is a reflection of ______.
- conservation of current density vector.
- conservation of charge.
- the fact that the momentum with which a charged particle approaches a junction is unchanged (as a vector) as the charged particle leaves the junction.
- the fact that there is no accumulation of charges at a junction.
विकल्प
b and c
a and c
b and d
c and d
उत्तर
b and d
Explanation:
Junction rule: At any junction, the sum of the currents entering the junction is equal to the sum of currents leaving the junction.
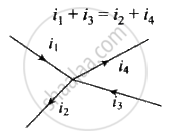
Or
Algebraic sum of the currents flowing towards any point in an electric network is zero, i.e., charges are conserved in an electric network.
The proof of this rule follows from the fact that when currents are steady, there is no accumulation of charges at any junction or at any point in a line. Thus, the total current flowing in, (which is the rate at which charge flows into the junction), must equal the total current flowing out.
Kirchhoff's junction rule is also known as Kirchhoff’s current law.
So, Kirchhoff's junction rule is the reflection of conservation of charge
Important point: Sign convention of current from a junction: We are taking outgoing current from a junction as negative. And we are taking incoming current towards a junction as positive.
APPEARS IN
संबंधित प्रश्न
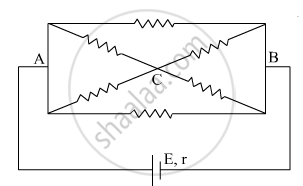
The current is drawn from a cell of emf E and internal resistance r connected to the network of resistors each of resistance r as shown in the figure. Obtain the expression for
- the current draw from the cell and
- the power consumed in the network.
A capacitor of capacitance 8.0 μF is connected to a battery of emf 6.0 V through a resistance of 24 Ω. Find the current in the circuit (a) just after the connections are made and (b) one time constant after the connections are made.
Two unequal resistances, R1 and R2, are connected across two identical batteries of emf ε and internal resistance r (see the figure). Can the thermal energies developed in R1 and R2 be equal in a given time? If yes, what will be the condition?
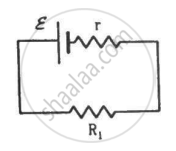
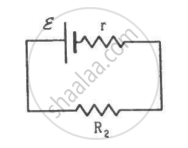
Solve the following question.
Using Kirchhoff’s rules, calculate the current through the 40 Ω and 20 Ω resistors in the following circuit.

The Kirchhoff's second law (ΣiR = ΣE), where the symbols have their usual meanings, is based on ______.
While measuring the length of the rod by vernier callipers, the reading on the main scale is 6.4 cm and the eight divisions on vernier is in line with marking on the main scale division. If the least count of callipers is 0.01 and zero error - 0.04 cm, the length of the rod is ______.
Three resistors having resistances r1, r2 and r3 are connected as shown in the given circuit. The ratio `i_3/i_1` of currents in terms of resistances used in the circuit is: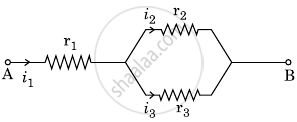
In a meter bridge the point D is a neutral point (Figure).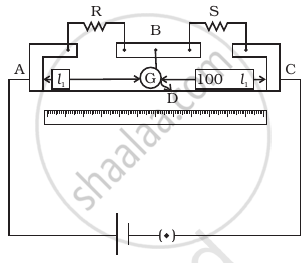
- The meter bridge can have no other neutral point for this set of resistances.
- When the jockey contacts a point on meter wire left of D, current flows to B from the wire.
- When the jockey contacts a point on the meter wire to the right of D, current flows from B to the wire through galvanometer.
- When R is increased, the neutral point shifts to left.
Two cells of voltage 10V and 2V and internal resistances 10Ω and 5Ω respectively, are connected in parallel with the positive end of 10V battery connected to negative pole of 2V battery (Figure). Find the effective voltage and effective resistance of the combination.
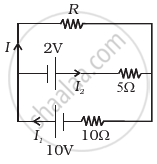
State the two Kirchhoff’s rules used in the analysis of electric circuits and explain them.
