Advertisements
Advertisements
प्रश्न
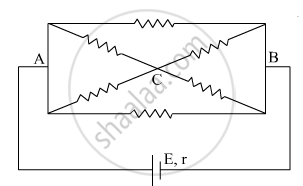
The current is drawn from a cell of emf E and internal resistance r connected to the network of resistors each of resistance r as shown in the figure. Obtain the expression for
- the current draw from the cell and
- the power consumed in the network.
उत्तर

From the above figure we can use the horizontal symmetry to deduce the current.
As both resistance in the circuit as well as the internal resistance in the circuit have the same resistance 'r'
The resistance of the loop I will be
`1/R_I=1/r+1/(2r)`
`1/R_I=(3r)/(2r^2)`
`R_I=(2r)/3`
Because the circuit I and II are same we can say
RII=(2r)/3
Combined resistance will be
R = RI + RII
`1/R=1/R_(I)+1/R_(II)`
`1/R=1/((2r)/3)+1/((2r)/3)`
`1/R=2×(1/((2r)/3))`
`R=r/3`
Now this circuit is series with internal resistance 'r'
Resultant resistance will be
`R_("resultant")=(4r)/3`
The current drawn from the cell will be
`I=(3E)/(4r)`
And power consumed by the network
`P=I^2/R`
`P=(9E^2)/(16r^2)×(4r)/3`
`P=(3E^2)/(4r)`
APPEARS IN
संबंधित प्रश्न
State Kirchhoff's rules and explain on what basis they are justified.
Consider the circuit shown in the figure. Find (a) the current in the circuit (b) the potential drop across the 5 Ω resistor (c) the potential drop across the 10 Ω resistor (d) Answer the parts (a), (b) and (c) with reference to the figure.
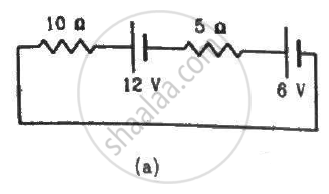
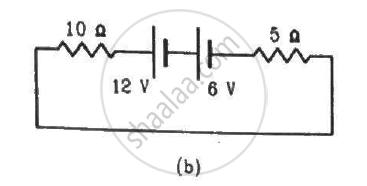
Two unequal resistances, R1 and R2, are connected across two identical batteries of emf ε and internal resistance r (see the figure). Can the thermal energies developed in R1 and R2 be equal in a given time? If yes, what will be the condition?
How the emf of two cells are compared using potentiometer?
A copper wire of 10-6 m2 area of cross-section, carries a current of 2 A. If the number of electrons per cubic meter is 8 × 1028, calculate the current density and average drift velocity.
The e.m.f of The battery in a thermocouple is doubled. The rate of heat generated at one of the junction will.
Three resistors having resistances r1, r2 and r3 are connected as shown in the given circuit. The ratio `i_3/i_1` of currents in terms of resistances used in the circuit is: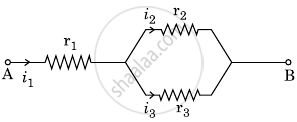
In a meter bridge the point D is a neutral point (Figure).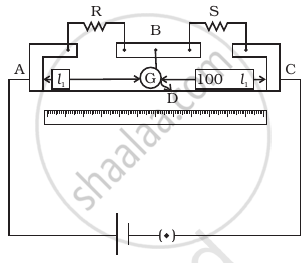
- The meter bridge can have no other neutral point for this set of resistances.
- When the jockey contacts a point on meter wire left of D, current flows to B from the wire.
- When the jockey contacts a point on the meter wire to the right of D, current flows from B to the wire through galvanometer.
- When R is increased, the neutral point shifts to left.
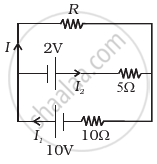
Two cells of voltage 10V and 2V and internal resistances 10Ω and 5Ω respectively, are connected in parallel with the positive end of 10V battery connected to negative pole of 2V battery (Figure). Find the effective voltage and effective resistance of the combination.
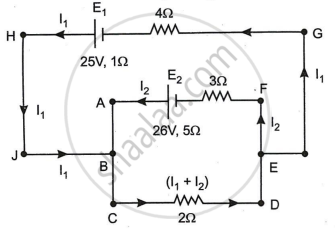
In the circuit shown in Figure below, E1 and E2 are batteries having emfs of 25V and 26V. They have an internal resistance of 1 Ω and 5 Ω respectively. Applying Kirchhoff’s laws of electrical networks, calculate the currents I1 and I2.