Advertisements
Advertisements
Question
Find an expression for maximum range of a particle which is projected with an initial velocity of ‘u’ inclined at an angle of ‘β’ with the horizontal.
Solution
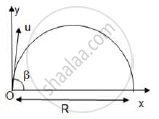
Consider a particle performing projectile motion.
R – Horizontal Range
T – Total flight time
Considering vertical components of motion,
`s =ut +1/2 at^2`
`0 " usin "(beta)-1/2 gT^2`
`T = (2usin(beta))/g`
Considering horizontal components of motion,
`s =ut +1/2at^2`
R = ucos(β)T + 0 …….(as acceleration in x direction is zero)
`"R = ucos"(beta)xx(2usin(beta))/g`
`R=(u^2sin(2beta))/g`
For maximum Range, sin(2β) should be maximum, i.e. sin(2β) = 1, i.e. 2β = 90, i.e. β=450
`R_(max)= u^2/g`
APPEARS IN
RELATED QUESTIONS
From (v-t) diagram find (1) Distance travelled in 10 second.
(2) Total distance travelled in 50 second.
(3) Retardation
Determine the speed at which the basket ball at A must be thrown at an angle 30o so that if makes it to the basket at B.
Also find at what speed it passes through the hoop.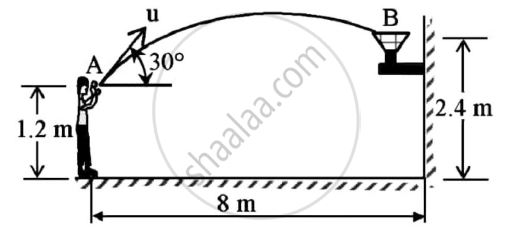
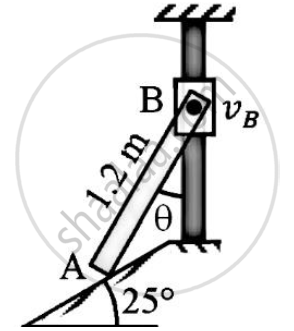
Figure shows a collar B which moves upwards with constant velocity of 1.5 m/s.At the instant when θ=50o.Determine :
(i)The angular velocity of rod pinned at B and freely resting at A against 25o sloping ground.
(ii)The velocity of end A of the rod.