Advertisements
Advertisements
Question
Find the force F4 , so as to give the resultant of the force as shown in the figure given below.
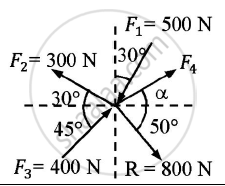
Given : Forces and their resultant
To find : Force F4
Solution
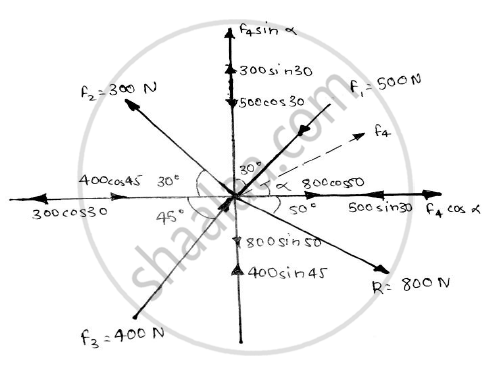
Assume that force F4 acts at an angle θ
Taking forces having direction towards right as positive and forces having direction upwards as positive.
Resolving forces along X direction :
`-F_1sin30 – F_2cos30 + F_3cos45 + F_4cosθ = Rcos50`
`-500sin30 – 300cos30 + 400cos45 + F_4cosθ = 800cos50`
F4cosθ = 741.195 …………(1)
Resolving forces along Y direction :
`-F_1cos30 + F_2sin30 + F_3sin45 + F_4sinθ = -Rsin50 ` `-500cos30 + 300sin30 + 400sin45 +F_4sin θ = -800sin50 ` F4sin θ = -612.6656 ……….(2)
Squaring and adding (1) and (2)
`(F_4sinθ)^2 + (F_4cos θ)^2 = (-612.6656)^2 + (741.195)^2`
`F_4^2(sin^2 θ + cos^2 θ) = 924729.1173`
`F_4 = 961.6284 N`
Dividing (2) by (1)
`(F_4sinθ)/(F_4cosθ) = (−612.6656)/(741.195) `
tan θ = -0.8266
θ = 39.5769o (in fourth quadrant)
F4 = 961.6284 N ( at an angle 39.5769o in fourth quadrant )
APPEARS IN
RELATED QUESTIONS
Find the resultant of the force system as shown in the given figure.
In the rocket arm shown in the figure the moment of ‘F’ about ‘O’ balances that P=250 N.Find F. 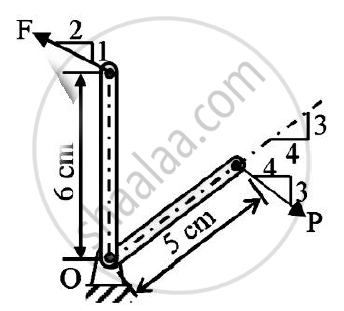
The resultant of the three concurrent space forces at A is 𝑹̅ = (-788𝒋̅) N. Find the magnitude of F1,F2 and F3 forces.

Given : A=(0,12,0)
B=(-9,0,0)
C=(0,0,5)
D=(3,0,-4)
Resultant of forces = (-788𝑗̅) N
To find : Magnitude of forces F1,F2,F3
