Advertisements
Advertisements
Question
Find the slope of a line passing through the following pair of points
(5pq,p2q) and (5qr,qr2)
Solution
A(x1,y1) = A(5pq, p2q)
B(x2, y2) = B(5qr, qr2)
Slope of line AB = `("y"_2 - "y"_1)/("x"_2 - "x"_1)``
= `("qr"^2 - "p"^2"q")/(5"qr" - 5"pq")`
= `("q"("r"^2 - "p"^2))/(5"q"("r" - "p"))`
= `1/5 (("r" - "p")("r" + "p"))/(("r" -"p"))`
= `("r" + "p")/5`
APPEARS IN
RELATED QUESTIONS
Find the slope of the line parallel to AB if : A = (−2, 4) and B = (0, 6)
The points (K, 3), (2, −4) and (−K + 1, −2) are collinear. Find K.
Angles made by the line with the positive direction of X–axis is given. Find the slope of these line.
60°
Find the slope of the lines passing through the given point.
L (–2, –3) , M (–6, –8)
Find the slope of the lines passing through the given point.
E(–4, –2) , F (6, 3)
Determine whether the given point is collinear.
\[P\left( 1, 2 \right), Q\left( 2, \frac{8}{5} \right), R\left( 3, \frac{6}{5} \right)\]
Find the slope of a line parallel to the given line x +3y = 7
Find the slope and the y-intercept of the following line x - 2 = `(5 - 3"y")/2`
Verify whether the following points are collinear or not:
A(1, –3), B(2, –5), C(–4, 7).
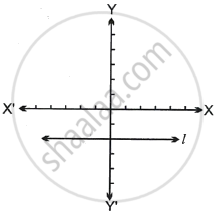
In the figure, line l is parallel to X-axis. Which of the following statement is true?