Advertisements
Advertisements
Question
Find the smallest number by which the given number must be divided so that the resulting number is a perfect square:
14283
Solution
For each question, factorise the number into its prime factors.
14283 = 3 x 3 x 3 x 23 x 23
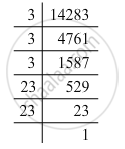
Grouping the factors into pairs:
14283 = (3 x 3) x (23 x 23) x 3
Here, the factor 3 does not occur in pairs. To be a perfect square, all the factors have to be in pairs. Hence, the smallest number by which 14283 must be divided for it to be a perfect square is 3.
APPEARS IN
RELATED QUESTIONS
Find the square root of the following number by the prime factorisation method.
5929
For the following number, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
2028
Find the smallest number by which the given number must bew multiplied so that the product is a perfect square:
23805
Write true (T) or false (F) for the following statement.
The number of digits in a square number is even.
Find the square root the following by prime factorization.
196
Find the square root the following by prime factorization.
4096
Find the square root the following by prime factorization.
8281
Find the square root the following by prime factorization.
24336
Find the square root the following by prime factorization.
3013696
Examine if the following is a perfect square
1089
